TIFR CSE 2015 | Part A | Question: 7

Question

A $1 \times 1$ chessboard has one square, a $2 \times 2$ chessboard has five squares. Continuing along this fashion, what is the number of squares on the regular $8 \times 8$ chessboard?

• A. $64$
• B. $65$
• C. $204$
• D. $144$
• E. $256$

Comments

I can solve this que with  the help of present of mind but why this que is the part of Permutations and combinations, where we are arranging and selecting.

Answer 1

Now lets see how many $7 \times 7$ squares are possible

 

These two patterns can shift to right as well as follows:

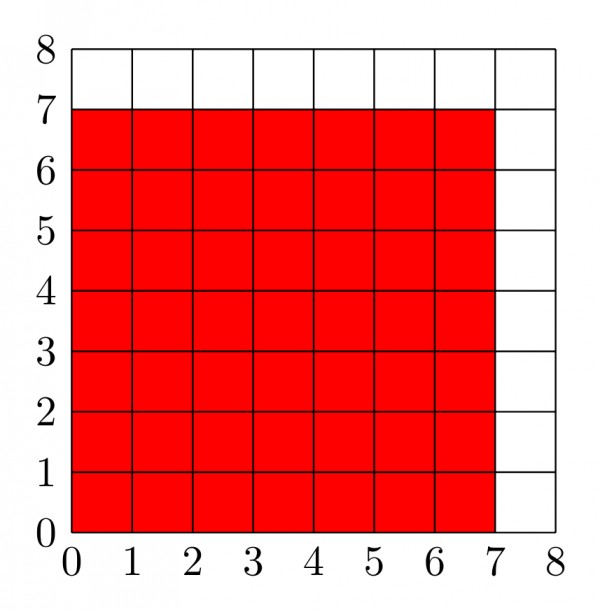
So, $7\times 7$ squares possible is $4$

Now lets see how many $6 \times 6$ squares are possible

 

So, $6\times 6$ squares possible is $9$

Now lets see how many $5 \times 5$ squares are possible:

$4$ vertical moves $\times  4$ horizontal moves $=4^2$ possibilities.

Proceeding like this,

• $8\times 8$  squares possible $: 1\times 1=1$
• $7\times 7$  squares possible $:2\times 2=4$
• $6\times 6$  squares possible $:3\times 3=9$
• $5\times 5$  squares possible $:4\times4=16$
• $4\times 4$  squares possible $: 5\times5=25$
• $3\times 3$  squares possible $: 6\times6 =36$
• $2\times 2$  squares possible $: 7\times7 =49$
• $1\times 1$  squares possible $:8\times8=64$

---

Total squares $\quad: 204$

Now we can generalize like with $n \times n$ chess board total squares $=1^2+2^2+3^2+\ldots +n^2 = \frac{n(n+1)(2n+1)}{6}$

Correct Answer: $C$

Comments

Similarly I have done

In $8\times 8$ chess board $1\times 1$ square possible 64, i.e. $8\times 8$

                                        $2\times 2$    square possible  $7\times 7$

 

Say if  in a chess board we give number of each point like this

 

1              2                3               4................................

 

2

 

3

 

4

.

.

then $2\times 2$ square go like this

1 to 3 is one square, 2 to 4 next square like this.

like this u go and get $7\times 7$ squares for $2\times 2$ matrix.

got it?

---

Ok.. Got it... Thanks for detailed explanation..

I have few more queries in combinatorics... Can I ask u by sending message

---

shortcuts:

total no of square possible in n *n chess board= (n(n+1)(2n+1))/6

total no of rectangles possible in n *n chess board= (n(n+1)/2)^2

Answer 2

No. of squares on chessboard of $n\times n$ is equal to sum of squares of $n$ terms for $8\times 8$ chessboard,

$\begin{align} &=\frac{n\left(n+1\right)\left(2n+1\right)}{6} \\&=\frac{8\times 9\times 17}{6}\\&=204.\end{align}$

Comments

Can u please explain why it worked this way

---

https://math.stackexchange.com/questions/178693/analysis-of-how-many-squares-and-rectangles-are-are-there-on-a-chess-board

Answer 3

Let T(n,n) be the number of squares in a n*n chess board.

T(1,1) = 1 

T(2,2) (i.e) number of squares in a 2*2 chessboard = number of squares in a 1*1 chessboard + 2²

Similarly T(n,n) = T(n-1,n-1) + n²  if n>2 with base conditions T(1,1) = 1 and T(2,2) = 5

Solving, we will get T(8,8) = 204.

                             

Comments

After solving the relation -:

T(n,n) = $n*(n+1)*(2n+1)/6$

---

Can u please explain what had insisted you to add "n^2" term to the recurrence relation ?

Answer 4

By simple observation it will be-

1^2 + 2^2+ 3^2+ ...................+ n^2.

where n is the size given, in the question its 8.

sum of squares of numbers.

Comments

Yeah!.

 # squres in 8 ⨉ 8 chessboard = 8² (1 ⨉1 squres) +7² (2⨉2 squares)+6² (3⨉3 squares)+5² (4⨉4 squares)

+ 4² (5⨉5 squares)+3² (6 ⨉6 squares)+2² (7⨉7 squares)+1² (8 ⨉8 squares) = 204