This answer is not directly related to the QS But this may help to view this problem in a recursive way.
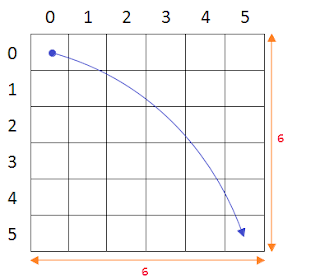
How many ways we can traverse this grid from $(0,0)$ to $(5,5)$.
Allowed moves from a cell are:
- Left to right by $1$ unit.
- Top to Bottom by $1$ unit.
This problem has $O(1)$ solution.
But we will see how we can use top-down recursion and memoization to calculate that value.
Currently, we have a problem size of $(6,6)$ i.e we have still to cover a $6^*6$ grid and we are at cell $(0,0)$.

Let's say we are at cell $(1,2)$ somehow.
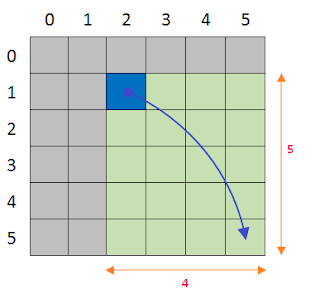
Now, this situation we have a $4^*5$ grid to traverse. What are the steps we can take in this cell or in this state ?
Well two things can be done.
- Go right
- Go down.
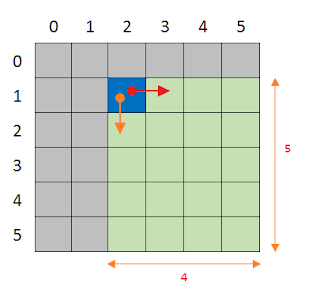
If we move right, then we will have to traverse a smaller grid of size $3^*5$

And if we move down, we will have to traverse a different smaller grid of size $4^*4$.

So, what we have seen is that from a bigger size problem of $4^*5$ grid we can arrive at smaller grid size problem by applying two different steps.
And if we sum up the two smaller subproblem solution we can get the result of bigger problem solution. (which was of size $4^*5$ ).
Therefore $\text{solution}(m,n) = \text{solution}(m-1,n) + \text{solution}(m,n-1)$, this is the recursion and the Top Down approach will seek for solution of $(m,n)$ without knowing the solution of $(m-1,n)$ and $(m.n-1)$. Using recursion we will recurse towards smaller and smaller sub problem untill we hit in some base case.
And the base here is:

When we arrive at cell $(5,5)$. In this state, we have arrived at the destination and there nothing to do now, and how many ways to go from $(5,5)$ to $(5,5)$. It is equal to $1$ ( means don't move in this particular case).
Therefore $ \text{solution}(1,1)$ $= 1$.
To speed up the solution and not repeating same sub problem, again and again, we will use memoization table.
Here is the code:
#define MAX_X 6
#define MAX_Y 8
int dp[MAX_X+1][MAX_Y+1];
int solve(int m,int n) {
if(dp[m][n] != -1) return dp[m][n];
int res = 0;
if(m > 1) res += solve(m-1,n);
if(n > 1) res += solve(m,n-1);
return dp[m][n] = res;
}
int main() {
for(int i=0;i<(MAX_X+1);i++)
for(int j=0;j<(MAX_Y+1);j++)
dp[i][j] = -1;
dp[1][1] = 1;
int m = MAX_X,n = MAX_Y;
printf("%d\n",solve(m,n));
return 0;
}