Correct Option: C
At first, draw two levels of the recursion tree:

Size of the problem will reduce as we go down a level each time in the tree.
Hence, in this case root will be the dominant part.
Final ans is $T(n) = \Theta (n)$ (order of the root) (you have to ans in less than $30$ sec!)
$\text{Let}\; f(n) = 1 + a + a^2 + \ldots + a^n, a<1 \\ \quad \implies f(n) = \frac{1 – a^{(n+1)}}{1-a}$
When $n \to \infty, f(n) = \frac{1}{1-a} = O(1)$ since $c = \frac{1}{1-a} $ is a constant.
We can see that the size of problem reduces geometrically, and root is the dominating part.
Note: Apply the following method for divide and conquer recursions because the size of the problem reduces geometrically. Not for subtract and conquer where it might reduce arithmetically!
And to apply this idea, all the conditions of Master theorem must be satisfied.
Everything given below is not required for GATE, it's just to explain the idea.
$T(n) = aT\left(\frac{n}{b} \right) + \Theta(n^k) \; , n>1$
$T(1) = c $
$($Assume all conditions of the Master theorem to be true here, $b>1).$
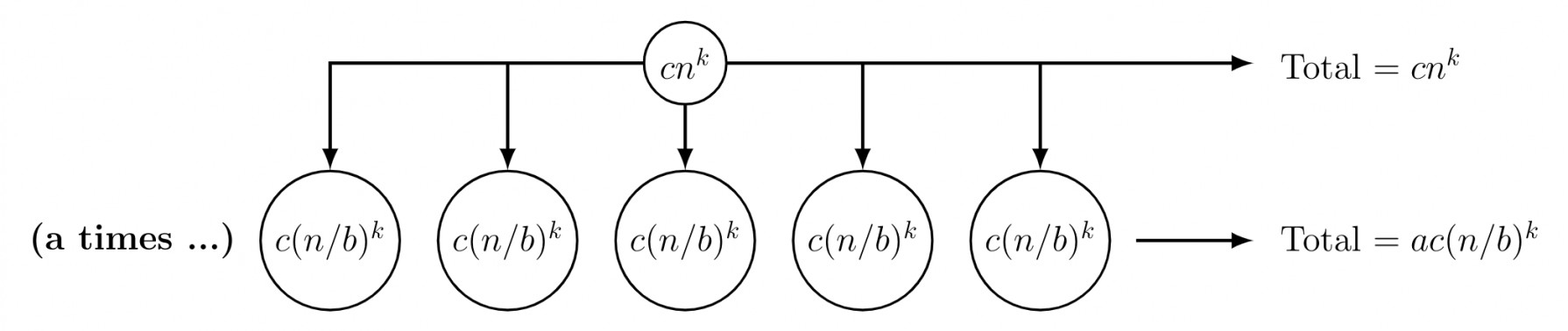
Let height of this tree be $h,$
$ \frac{n}{b^h} = 1 \implies b^h = n \implies h = \log_b(n) $
No. of leaves $= \underbrace{a*a*a*\ldots * a}_{\text{times the height of the tree}}= a^{\log_b(n)} = n^{\log_b(a)}$
Here’s the relation with master theorem:
Case 1 (root is dominant): $cn^k > ac\left(\frac{n}{b}\right)^k $
$ \implies 1 > \frac{a}{b^k} \implies b^k > a \implies \boldsymbol{k > \log_b(a)}$
$\implies n^k > n^{\log_b(a)}$
This case of Master theorem says $T(n) = \Theta (n^k)$, which is nothing but the order of root.
(We are kinda deriving cases of the master theorem using intuition)
Case 2 (root is equal to all levels): $cn^k = ac\left(\frac{n}{b}\right)^k $
$ \implies 1 = \frac{a}{b^k} \implies b^k = a \implies \boldsymbol{k = \log_b(a)}$
$\implies n^k = n^{\log_b(a)}$
According to the Master theorem, $T(n) = \Theta (n^k \log(n))$.
All the levels are equally dominant, hence final result will be the sum of all levels. That is,
size of a particular level $\times$ the height $\implies n^k\times\log_b(n)$, Hence $T(n) = \Theta (n^k \log_b(n))$.
Case 3 (leaf level is dominant):
$\implies 1 <\frac{a}{b^k} \implies b^k < a \implies \boldsymbol{k < \log_b(a)}$
$\implies n^k < n^{\log_b(a)}$
According to Master theorem, $T(n) = \Theta (n^{\log_b(a)})$
As the leaves’ levels are dominant, Ans will be in the order of the leaf’s level = Order of no of leaves in the tree (because base condition will be a constant)
Hence $T(n) =\Theta (n^{\log_b(a)})$
After reading this logic you’ll never have to remember the Master theorem!
Reference
You’ll find different kind of recurrence relations and how to solve them here: