GATE CSE 2014 Set 3 | Question: 39

Question

Suppose we have a balanced binary search tree $T$ holding $n$ numbers. We are given two numbers $L$ and $H$ and wish to sum up all the numbers in $T$ that lie between $L$ and $H$. Suppose there are $m$ such numbers in $T$. If the tightest upper bound on the time to compute the sum is $O(n^a\log^bn+m^c\log^dn)$, the value of $a+10b+100c+1000d$ is ______.

Comments

During inorder traversal if we take elements between L and H then it take O(n) time(time for in order traversal) then why we do some extra work and pay extra cost O(log n). Because L and H is already given and L and H need not be in BST.

So answer is a=1 , b=0, c=0, d=0.

We can't take 'm' ='n' because in worst case all tree elements sum up.

---

Confusing question: https://gateoverflow.in/18749/tifr2010-b-26

Similar question: https://gateoverflow.in/333190/gate-2020-cse-question-41

---

Can it be done this way?

A hash table of size H can be initialized. // O(H) Space, let the table be Arr[H+1]
Next, all of the nodes till the target node can be marked visited in the table. O(logn) for 2 searches. (Remember, the nodes shall be only marked visited if were not visited before, to get rid of duplicate entries).
Finally, the hash table can be traversed, and the visited node’s sum can be calculated. // Start visiting from Arr[L]
Time Complexity : O(m+logn).
Auxiliary Space: O(H).

Answer 1

In worst case for finding $L$ and $H$ it will take $O(\log n)$ time as the given tree is balanced binary search tree.
Now there are $m$ elements between $L$ and $H$. So to traverse m element it will take $O(m)$ time (traversal algorithm given below). So, total

$O(m+\log n)  \implies a=0, b=1,c=1,d=0$
$\therefore 0+(10 \times 1)+(100 \times 1)+(1000 \times 0)=110$. 

---

To find all the numbers from $L$ to $H$ we can do an inorder traversal from root and discard all elements before $L$ and after $H$. But this has $O(n)$ time complexity. So, we can do a modification to inorder traversal and combine with binary search as follows:

1. Find $L$ using binary search and keep all nodes encountered in the search in a stack. 
2. After finding $L$ add it to stack as well and initialize $\text{sum} = 0$.
3. Now, for all nodes in stack, do an inorder traversal starting from their right node and adding the node value to sum. If $H$ is found, stop the algorithm. 

Comments

Point 3, you are saying do inorder traversal starting from the right node until H is encountered. It is for all values encountered in stack. Then i think time complexity will be more.

---

Sir, the tree is a balanced BST unlike the one you've drawn.

---

@kalpish, can you elaborate this stack using concept with some example? see this discussion on group.

https://www.facebook.com/groups/core.cs/permalink/1316231181742465

---

See we can understand like this :

First in order to find number which is labelled L , it will O(logn) time as it is a balanced BST.Then to add the m numbers between L and H , we use the modification of inorder traversal which will hence take O(m) time.Hence the value of a = 0 , b = 1 , c = 1 and d = 0 Hence the answer is 110.

---

I think while searching L we should not keep all the elements in the stack. Only the elements which are greater than L has to  be kept.
Otherwise we may be adding values smaller than L or sometimes same values more than once.

While searching for 15, we should not add 10 to the stack.

---

Impeccable explanation! Thanks a lot...

---

How can we start inorder from L?

anyhow we have to reach L first!

---

For reaching L log n is time, as explained in answer. Sorry for previous comment stack will be required.

---

why answer isn't 1100-(c=1,d=1)

Balanced BST takes logn time and for each m element it takes O(mlogn)

---

For each m element it does not take mlogn.

Search for L in Balanced Binary Search Tree = O(Log n)

Now, start taking inorder elements of the balanced tree, one by one. In each iteration you compare the element you got with L and H. If the element is between L && H then add it to the sum.

Hence, after inorder traversal is complete, you will have the sum (no need to complete inorder traversal till n elements since we are concerned only till m).

Total time taken = Time to search L + inorder Traversal of only m elements

O(logn + m)

---

DFS takes $O(x +y)$ time where $x$ is the number of nodes and $y$ is the number of edges. What to do with the $y$? No information is given in the question. Should we ignore it? Or can we do it like this:
A tree with $m$ nodes has $m - 1$ edges, so $O(x + y)$ becomes $O(m + m - 1) \rightarrow O(2m -1)=O(m)$.

---

Think like this

(1)L and H don't exist in the tree.

(2)L and H are the lowest and the highest data value respectively in balanced bst.

For case1: First before finding sum I need to make sure whether my L and H exist in BST or not. If they don't exist, then I won't execute my code for finding the sum. So, TC for finding L and H in Balanced BST is $O(logn)$

This is obviously not the worst case.

Case 2: Worst Case: First find L and H->$O(logn)$

Say, all n nodes lie between L and H. Now I need to find sum of all numbers in BST.

Do Inorder traversal in $O(n)$ time.

Total time complexity : $O(logn+n)$

---

In most of the answers and cooments it is said that " we can find L in O(Log n) and O(m) for sum".

I am not getting why and how it is O(m) ?

How traversal is applied on m elements ??

---

we already know L number then why we search it...why can't we do directly inorder traversal and add numbers after L

---

@Ayush Upadhyaya

After finding L ...in logn time ..we should apply inorder tranversal from node L..as we want nos > L and <H

and we can continue adding till we reached H..it wll take O(m) right ??

---

@Ayush Upadhyaya

If BST is given instead of BBST/AVL

Then O(n) [worst case to search L] + O(m) (indorder) ==> O(n)  ???

---

@jatin khachane 1-Yes I think so.

---

In the worst case, all elements might be present in between L and H, then it should take O(n) time to sum it up

---

@Ayush Upadhyaya 's comment is the perfect answer.

It will $\mathbf{O(n)}$ in the worst case and not $\mathbf{O(m)}$

---

I am still doubtful whether its $\mathbf{O(m)}$ or $\mathbf{O(n)}$ in the $\mathbf{Worst\;Case}$.

Can someone can clarify this.

@ankitgupta.1729

@Satbir

@srestha

@VS

@Ayush Upadhyaya

@Verma Ashish

Shaik Masthan

---

@`JEET it will be O(m).

We will first find L. As it is a BBST so it will take logn time. Now as you get L. From that node you apply inorder traversal upto H(it is given to us so no need to go further. Stop as you get H). Initialize a variable sum and add the nodes value encountered in the traversal to sum. Hence just m elements not n.

How inorder traversal after L-

I am applying inorder traversal in above tree drawn by Rajendra Dangwal see above comments.

You got L=15. Now do inorder from L. Take H=28

20,22,25,26. You got 28 stop algorithm further. And add nodes to variable sum. So we traversed m elements between L and H not n elements.

Time= O(logn+m)

Hope it helps.

---

Can anyone help me in understanding what is the significance of maintaining a Stack and doing inorder traversal for each element (which is added to Stack) from Right Child?

---

Why are we assuming that L and H are present in the tree? Am I missing something here?

---

read the qsn

---

@Jeet 

Say, all n nodes lie between L and H

Above statement was assumed by @ayush, hence O(n).

Given in question,

Suppose there are m such numbers in T

Hence worst case would be O(m) but not O(n).

---

For those wondering “why we need a stack to find the numbers b/w L and H, why can’t we just do the inorder traversal from L to H?”. Note that the inorder traversal needs a root node, it traverses only the nodes occurring below it, now even if we take L as the root node, we can’t traverse the nodes occurring above L in the original graph (See the trees given in other comments). So we need a stack whose elements act as the root nodes for various separate inorder traversals we do to find all nodes b/w L and H.

Hope it helps someone...

---

@Ayush Upadhyay The worst case will be when L and K are present in the BST. But what will be the time complexity when L and K are not in the list(which is not the worst case). Will it be O(n) because we have to traverse the whole BST in order to get the sum of the elements which lie between L and K?

---

@shraddha_gami.

we are not doing it simultaneously . it is one after the other that’s why O(logn+m) and not O(mlogn).

---

bro i dont understand the difference between

those O(mlogn) and O(m +logn) for what u’ve said

for traversing to an element which is between L and H it takes logn time right?

then for m such elements it would be mlogn only right?

thats what i thought

if u see this please help me in making me understand my mistake brother

that would be helpful for my preparation for GATE this year 2024

---

# Please look into this.

def inorderTraversal(self, root, L, H):
        tot_sum = 0
        stack = []
        cur = root
        while stack or cur:
            if cur:
                stack.append(cur)
                cur=cur.left
            else:
                cur=stack.pop()
                if cur.val >= L and cur.val <= H:
                    tot_sum += cur.val
                cur=cur.right
        return tot_sum

 

What about my code. 

Its O(n) and the sum is directly calculated. In worst case m = n, so your algorithm O(m + logn) will be same as mine. Doesn't the ques ask about the worst case.

Answer 2

Here is an example 😊

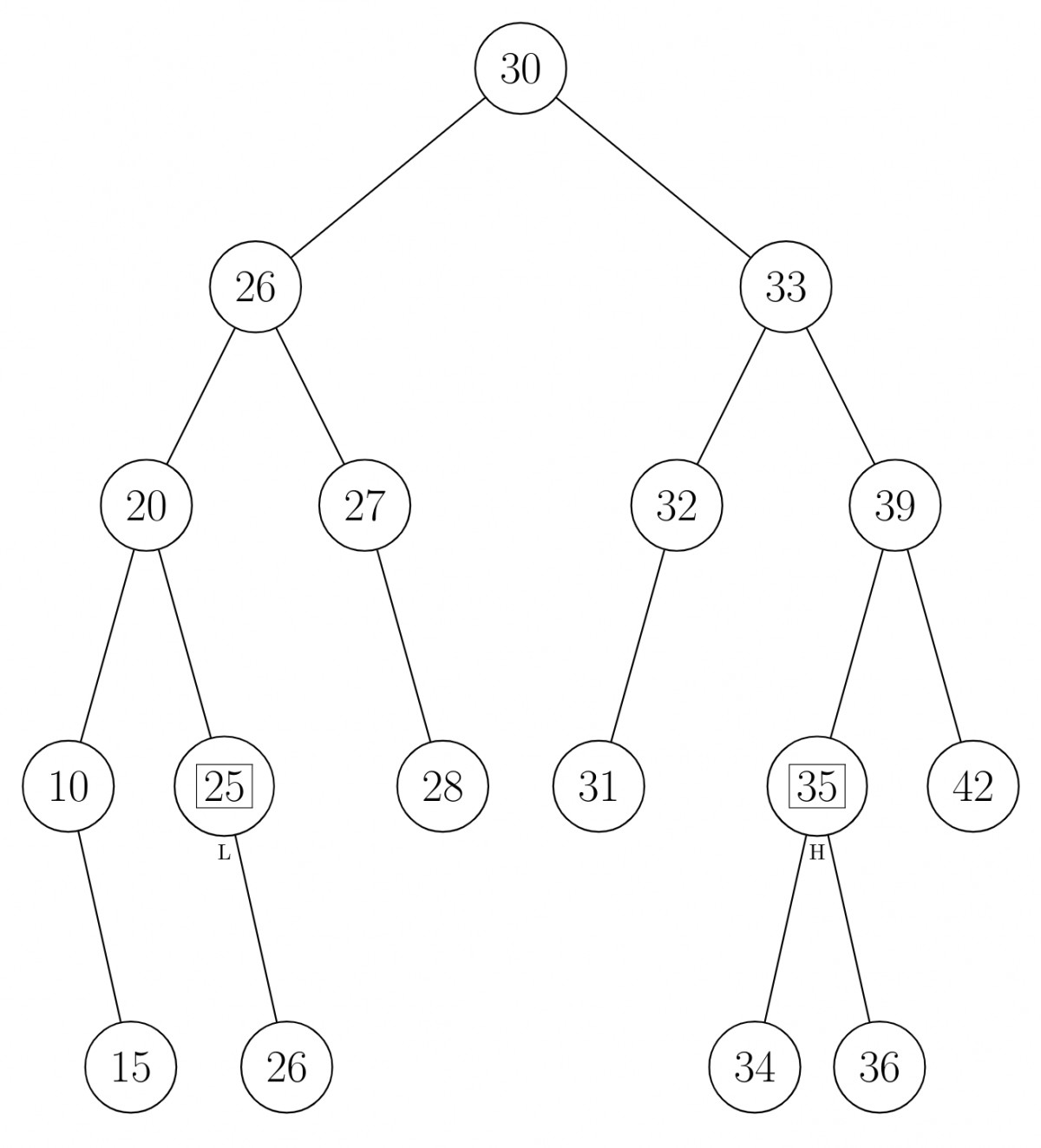
$L =25 , H = 35$
Inorder: $10,15,20,\underset{L}{\boxed{25}},26,27,28,30,31,32,33,34,\underset{H}{\boxed{35}},36,39,42$

1. Find $L$ and $H \rightarrow O(\log n)$ time.
2. Traverse '$m$' elements between '$L$' and  '$H$' $\rightarrow O(m)$ [Traversal algorithm]

Total $\rightarrow  O(m + \log n) $

$\qquad a= 0,b=1,c=1,d=0$

$\qquad 10 + 100 = 110$ Answer

Traversal Algorithm:

1. Find $L$ using Binary search and keep  $H>node> L$ encountered in the search in a stack.
   
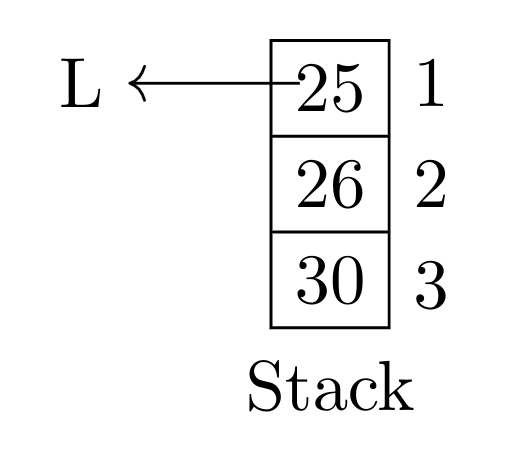
2. After finding $L,$ add it to stack as well & initialize $sum = 0$
3.  Now, for all nodes in the stack, do an inorder traversal starting from their right node and adding the node value to sum. If it is found than stop the algorithm.

• Node (1) 
  • No Right child; Sum = Sum + Node value $= 0 + 25 = 25.$
• Node (2)
  • Inorder Traversal from Right Child $\rightarrow  24,28$
  • Sum = sum + inorder Traversal + Node Value $=  (25 + 27 + 28) + 26$
• Node (3)
  • Inorder Traversal From Right Child $\rightarrow 31,32,33,34,\overset{H}{\bf{35}}\overset{\to \text{Stop Inorder Traversal}}{}$
  • Sum = Sum + Inorder Traversal + Node value
    • $\qquad = 25 + 26 + 24 + 28 + (31 + 32 + 33 + 34 + 35) + 30$
    • $\qquad = 25 + 26 + 24 + 28 + 30 + 31 + 32  + 33 + 34 + 35$  Answer

---

EDIT :

1. In Step 1, we need to find only $L$ and not $H.$
2. In Traversal Algo: Find $L$ using Binary Search and Keep, L< Nodes< H, encountered in the search in the stack.

Comments

Why only $25,26,30$ elements added into the stack?

---

Shiva Sagar Rao since its doing binary search to find L ..i.e. 25

so it will get to 30 first (mid) then left….of that since 25<30..so we will get 30,26,25…

 

But i have one doubt..

in this algorithm why we are assuming inorder traversal is given??

to find inorder traversal to get sorted numbers ..it will take O(n) right?

 

---

thanks.

Answer 3

int getSum(node *root, int L, int H)
{
   // Base Case
   if (root == NULL)
      return 0;

   if (root->key < L)        
       return getSum(root->right, L, H);

  if (root->key > H)
      return getSum(root->left, L, H)

   if (root->key >= L && root->key <=H)        
      return getSum(root->left, L, H) + root->key +
             getSum(root->right, L, H);
}

it will be O(logn +m)

it can go max of logn depth to find nodes in range and  function calls for nodes in range ie m

Note that the code first traverses across height to find the node which lies in range. Once such a node is found, it recurs for left and right children. Two recursive calls are made only if the node is in range. So for every node that is in range, we make at most one extra call (here extra call means calling for a node that is not in range).

source:http://geeksquiz.com/gate-gate-cs-2014-set-3-question-49/

Comments

Thanks for valuable effort.

---

So in worst case 'm' can equal to 'n', right?

---

# Please look into this.

def inorderTraversal(self, root, L, H):
        tot_sum = 0
        stack = []
        cur = root
        while stack or cur:
            if cur:
                stack.append(cur)
                cur=cur.left
            else:
                cur=stack.pop()
                if cur.val >= L and cur.val <= H:
                    tot_sum += cur.val
                cur=cur.right
        return tot_sum

 

What about my code. 

Its O(n) and the sum is directly calculated. In worst case m = n, so your algorithm O(m + logn) will be same as mine. Doesn't the ques ask about the worst case.

Answer 4

Do tree traversal from root as follows: Do a recursive search to find L, saving all the nodes visited in a stack. Since tree is balanced BST, it'll take O(log n) time. After finding L instead of search do inorder traversal up to m nodes from this node and continuing (if needed) using the saved nodes during searching. Complexity O(m).

Total time = O(m) + O(log n)

a=0, b=1, c=1, d=0
a+10b+100c+1000d = 0+ 10 + 100 + 0
= 110

Comments

@Rajesh Pradhan sir, I have the same confusion. Have you got it now? Why is stack required here?

Just in case you read this, can this problem be solved by just finding L $[O(logn)\ time]$, then performing an inorder traversal for m+1 numbers $[O(m)\ time]$; then adding them up $[O(1)\ time]$

My point is, can it be solved simply like that, or am I missing something?

---

@JashanArora adding to your points, I think your approach is valid we just need to make sure that the values < L in inorder traversal must be dropped. Finally according to me we can solve it without using stack in the following way:

 

1. First find the value of L.

 

2. Now

IF  L has right node then initialise sum = L  ELSE sum = 0.

 

3. Now

IF  if L has right node do inoder traversal starting from the L's right node and keep on incrementing sum (making sure visited node values are >=  L if not then ignore those values ) with visited node value until we reach H. 

 

ELSE L itself is the right node so start inorder traversal from L itself and keep on incrementing sum ( again making sure visited node values are >=  L if not then ignore those values ) with visited node value until we reach H.

 

4. finally sum value is our answer.

 

@DigvijayPandey sir, @Arjun sir or anyone please correct me if I am wrong.

---

@Aadesh

This is wrong how can you do in-order traversal starting from L, as L will contribute a sub-tree of the whole. That’s why stack is needed to store the nodes that were visited before L.

And instead of ignoring values that are smaller than L , just do the in-order traversal of right-subtrees