GATE CSE 2020 | Question: 39

Question

Which one of the following predicate formulae is NOT logically valid?

Note that $W$ is a predicate formula without any free occurrence of $x$.

• A. $\forall x (p(x) \vee W) \equiv \forall x \: ( px) \vee W$
• B. $\exists x(p(x) \wedge W) \equiv \exists x \: p(x) \wedge W$
• C. $\forall x(p(x) \rightarrow W) \equiv \forall x \: p(x) \rightarrow W$
• D. $\exists x(p(x) \rightarrow W) \equiv \forall x \:  p(x) \rightarrow W$

Comments

@Suraj Reddy, For null quantification rules, $W$ can have free variables in it, but $W$ should not have a free variable $x.$ The same proof will work, but one statement we will have to add (or implicitly keep in the back of our mind) before the proof is “for any value-assignment to all the free variables of $W$, either $W$ will be True or $W$ will be false”. 

If $W$ has some free variable(s), say $y$, then LHS & RHS both will be Predicates over variable $y$, not propositions, But that is fine because we only find equivalence of LHS & RHS.  

See THIS example. See THIS also. 

---

@Deepak Poonia So, either $W$ is a quantified predicate formula, or $W$ has some other free variable y but not x where we can think(of the option A) as $\exists y \forall x(p(x)\vee W)  \equiv \exists y (\forall xp(x)\vee W)$. Just finding equivalence between predicates doesn’t make sense.

---

@Suraj Reddy, I think the usefulness of predicate-equivalence comes during inference of one statement from a set of given statements. More about the usefulness of equivalence of predicates I will need to check. But the concept is what I have mentioned in the previous comments & in this lecture. 

Answer 1

(A)Let's consider two cases.

W-True.This makes both LHS and RHS True.
W-False.The value of LHS depends upon the truth value of $\forall$xP(x). Same will be the case for RHS.
Hence LHS =RHS.

(B)Using analogy in (A), we can prove that this is also valid.
W-True.LHS=RHS=True
W-False.LHS=RHS=False always.

(C)$\forall x(P(x) \rightarrow W) \equiv \forall xP(x) \rightarrow W$

LHS can be re-written as $\forall x(\lnot P(X) \lor W) \equiv \exists xP(x) \rightarrow W$

(C) is not logically valid.

(D)$\exists x(P(x) \rightarrow W) \equiv \exists x(\lnot P(X) \lor W) $

Using Demorgan law for quantifiers we can again rewrite it as:

$\lnot \forall x P(x) \lor W \equiv \forall x P(x) \rightarrow W$

Option (D) is valid.

Comments

how D is valid ??

---

Option D should be invalid

---

can somebody explain how D is invalid?
I had marked it as D.

---

> but the implication on RHS will be True.

It does not seem to be True, can @pradhanaditya prove it using those two variables as described?

---

(D) $\exists x (p(x) \rightarrow W)$
      $\exists x (\neg  p(x) \vee  W)$
      $(\exists x\; \neg  p(x)) \vee  W$  
      $(\neg \forall x \neg\; (\neg  p(x))) \vee  W$
      $(\neg \forall x \;p(x)) \vee  W$
      $\neg (\forall x \;p(x)) \vee  W$
      $(\forall x \;p(x)) \rightarrow  W$
      $\forall x \;p(x) \rightarrow  W$  
      
So, LHS $\equiv$ RHS       

(C)  $\forall x \;(p(x) \rightarrow W) $
       $ \forall x \;(\neg\;p(x) \vee W)$
       $ (\forall x \neg p(x)) \vee W$
       $ (\neg\exists x \neg  \neg p(x)) \vee W$
       $ (\neg\exists x p(x)) \vee W$
       $ \neg(\exists x p(x)) \vee W$
       $ (\exists x p(x)) \rightarrow W$
       $ \exists x p(x) \rightarrow W$

So, in given question,  LHS $\not\equiv$ RHS

From Kenneth H. Rosen (Question 49) :  https://gateoverflow.in/?qa=blob&qa_blobid=10691577044077116257

---

I reviewed the solution manual to Kenneth Rosen as well. Option (D) is proved invalid.

---

@shashin, in question (49), we don't have to prove valid or invalid. We have to establish logical equivalences. Means these are true. Right ?

---

I apologize, bad choice of words - I mean to say Option (D) is proved logically equivalent in that question (49(b)), hence does not seem to be the answer to this question :)

---

https://ia800409.us.archive.org/12/items/DiscreteMathematicsAndItsApplications7thEditionKennethH.RosenStudentsSolutionsGuidel/Discrete%20Mathematics%20and%20Its%20Applications%20%5B7th%20Edition%5D%20-%20Kenneth%20H.%20Rosen%20Students%20Solutions%20Guidel.pdf

Page 31 of the pdf (page 22 of the book)

---

@ankitgupta.1729

@shashin

what about option A)??

for all x(A or B) Can it be equal to for all x A??

Say we take a set S={2,3}

Now, A is divisible by 2 and B is divisible by 3.

Now, it is supporting LHS, but not RHS

right??

 

---

sorry ma'am, I am not getting you.

In (A),

$\forall x(p(x) \vee W) =(p(x_1) \vee W)\wedge (p(x_2) \vee W)\wedge(p(x_3) \vee W)\wedge.... $

Now, Using Distributive Law i.e. $(p \vee q)\wedge (p \vee r) \equiv p \vee (q\wedge r) $

The above expression can be written as :

$\Leftrightarrow ((p(x_1)\wedge p(x_2)\wedge p(x_3)\wedge........ )\vee W )$

$\Leftrightarrow ((\forall x\;p(x))\vee W )$

$\Leftrightarrow\forall x\;p(x)\vee W $

---

@ankitgupta.1729

u proved it by formula

But, if I want to prove it logically.

Say there is a set S , whose elements are x, and x is either divisible by 2 or divisible by 3.

So, element of set is p(x) which is divisible by 2

and W  , which is divisible by 3.

Now for option A LHS ="there is a set S , whose elements are x, and x is either divisible by 2 or divisible by 3"- this statement is valid.

But for RHS, it is telling, for all x, x is divisible by 2, which is not correct.

So, A) seems invalid

---

@ankitgupta.1729

In C)

$LHS:\forall x (p(x)\rightarrow W) \equiv \forall x(\neg p(x) \vee W) $

$RHS:\forall x\:p(x) \rightarrow W \equiv \neg [\forall x\: p(x)] \vee W = \neg \forall x \neg p(x) \vee W \equiv \exists x \neg p(x)\vee W $

Now, it is telling LHS "for all x either p(x) is not exists or W exists"

And "for some x either p(x) is not exists or W exists " 

Now, how it could be more appropriate answer than A)??

@shashin

Which example of Kenneth Rosen u suggest for option A) and C)

---

@srestha ma'am

Suppose, p(x) means x is divisible by either 2 or 3.

Suppose, domain contains elements {2,3,4,5,6,7}

Now, in option (A),

LHS is : $\forall x(p(x) \vee W) =(p(x_1) \vee W)\wedge (p(x_2) \vee W)\wedge(p(x_3) \vee W)\wedge (p(x_4) \vee W)\wedge (p(x_5) \vee W)\wedge (p(x_6) \vee W)\wedge (p(x_7) \vee W)$
Now, here, $p(x_1) = T, p(x_2) = T, p(x_3) = T, p(x_4) = F, p(x_5) = T, p(x_6) = T, p(x_7) = F$

Now, Take 2 cases when  W = True and W=False and put truth values in both cases and find resultant truth value.

When W= True then resultant truth value will be True and when W=False then resultant value will be False.

Now,

RHS is : $\Leftrightarrow ((p(x_1)\wedge p(x_2)\wedge p(x_3)\wedge........ )\vee W )$

Here, when W=True then whole expression gives True

and when W=False then whole expression gives False.

Understood ?

---

@ankitgupta.1729

Is not option A) very similar to this question https://gateoverflow.in/256/gate1992-92-xv

See in this question option C),it is same as option A) here

If that question, we are telling , it is not valid, then how it could be valid here??

---

ma'am, both are different questions.

---

why different? ? Where is difference??

---

That is a completely different question having very little in common with this one. That question deals exclusively with predicate functions with bound variables. This one deals with bound and free variables. The dynamics change quite a bit.

Not a good idea to compare the two.

---

but I want to know, logically where is difference?

Even in Rosen , I havenot got cleared how A) would be valid.

---

I will not try to explain Rosen examples. That is a standard text book and I cannot do a better job of explaining it than Rosen does. And Ankit has done a good job of answering this question in the comments above.

But I will give you two statements to help you see the difference between this question and the one you linked:

$\forall(x)(P(x) \rightarrow Q)$ and $\forall(x)(P(x) \rightarrow Q(x))$

There is a big difference between these two statements. What is it ?

---

x missing, but why is it big difference?

---

Lets try them in some real sentences,

suppose, $P(x) =$ $function$ which returns $true$ if $x$ is $even$ else returns $false$. 

and, $W =$ $function$ which returns $true$ if it rained today else returns $false$ (lets call it $Rain()$)

 

Now, in option $C$ we have,

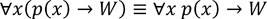
$LHS$ : For all the individual $x$ (either that particular $x$ is odd or $Rain()$)

$RHS$ : either there exists a odd number $x$ or $Rain()$.

 

An example where $LHS$ and $RHS$ are different:

set of $x = \{2,3, 4\}$

$LHS = Rain()\ and\ True\ and\ Rain()$ ($and$ because it must be true for all $x$)

$RHS = True$ (since 3 is in the set and is odd)

Now if it didn't rain today, then $LHS$ will become $False$ hence it cannot be equal to $RHS$ which is definitely $True$.

(Note, LHS and RHS should be equal for all possible values of $Rain()$ and it clearly isn't same if $Rain()$ returned $false$)

 

Lets check option $A$,

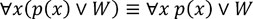
$LHS$ : For all the individual $x$ (either that particular $x$ is even or $Rain()$)

$RHS$ : either all of the $x$ are even or $Rain()$.

 

Lets try them on the same set as in previous case:

set of x = $\{2,3,4\}$

$LHS$ = $True\ and\ Rain()\ and\ True$ = $Rain()$

$RHS$ = $Rain()$ 

Here $LHS$ = $RHS$  (but maybe we didn't try hard enough to come up with a counter-example where they are not valid, you may try any possible set of $x$ and you will notice they will always be valid, there are only $3$ more cases to try, I will leave that as an exercise)

 

---

LHS : For all the individual x (either that particular x is even or Rain())

RHS : either all of the x are even or Rain().

yes, that makes option A) invalid. 

---

How does it make A invalid, I couldn't find any counter example, the set of x I took was valid. Can you think of a set for which it is invalid?

---

@mkagenius

See, here 

LHS : For all the individual x (either that particular x is even or Rain())

So, here  take x as {1,2,3 } 

Now take 1 and Rain(), where Rain() is true, So, $1V true=true$

Now take  2 and Rain(), where Rain() is False, So, $2V False=true$

Now take 3 and Rain(), where Rain() is true, So, $3V true=true$

So, Set {1,2,3} is a valid set.

But for RHS {1,2,3} is not a valid set, if Rain() is False sometime

 

---

You can't take different values for Rain(). Take one value and use it, either take it as true or take it as false. In a logical circuit a switch can't be both true and false.

---

Finally - you said it :)

This is exactly what I was trying to say earlier 

$\forall(x)(P(x) \rightarrow Q)$ and $\forall(x)(P(x) \rightarrow Q(x))$

There is a big difference between these two statements. What is it ?

One of them is a function of $x$ and as such, is bound by the quantifiers and all associated rules are applicable. The other one is pretty much a boolean variable.

---

I have proved that , Why cannot I do that? That is  valid thing

@shashin

That is just an instance, I am not telling both are exactly similar, but both can proved false by almost similar reason

---

Schrodinger's cat agrees with you but the normal world doesn't behave like that, as I said a switch (Rain()) cannot have two values at the same time. It will either rain today or it will not. It cannot both rain and not rain at the same time, its not schrodinger's 🐈

---

Okay I am at my wit's end here. You need to accept mathematical notation. That is not open to interpretation.

There is a difference between $W(x)$ and simply $W$. What is given in the question is $W$, and NOT $W(x)$

1. $W(x)$ - this is a FUNCTION of each instance of $x$, and can be either true/false for each and every single value of $x$. 
   • $\forall(x)W(x)$ is true only if $W(x)$ is true for every instance of $x$
      
2. $W$ - this is NOT A FUNCTION of each instance of $x$. For the entire domain - $W = true$ OR $W = false$. i.e. it is like a boolean variable.
   • If you consider $W = true$, $\forall(x)W$ is true. Period.
   • If you consider $W = false$, $\forall(x)W$ is false. Period.

You cannot say $W = true$ for $x_1$ and $W = false$ for $x_2$. There is nothing to prove here - it is widely accepted mathematical notation.

---

That is just an instance, I am not telling both are exactly similar, but both can proved false by almost similar reason

But this is discrete math. There is no concept of "similar". If someone shows you a cat and says it is a cat, you have to accept it is a cat. You cannot say "it has fur, a tail, and with some time I can teach it to bark - so it can be a dog as well". Doesn't work like that no :)

---

sir plz solve option c and d by taking some example. sir i am getting d as invalid .plz help me

---

Option A and B also not valid becos in option A ForAll distributed over conjunction (OR) which is incorrect.

In option B Exential distribute over disjunction which is also incorrecto or not valid statement????

---

Hi Sir, At Line 10 it should be ∀x(¬P(X)∨W)≡¬∃xP(x)∨W right?

---

Thanks @ shashin

---

@Ayush Upadhyaya, @Arjun Sir, @Lakshman Patel RJIT In option C, it must be $\forall x(\lnot P(X) \lor W) \equiv \forall x(\lnot P(X)) \lor W \equiv\lnot (\exists xP(x) )\lor W \equiv \exists x P(x) \rightarrow W$ which is !=RHS. That’s why Option C is not logically valid. It needs edit.

---

@Abhrajyoti00

That’s right what you have pointed out. The answer has been corrected.

Detailed Video Solution: https://www.youtube.com/watch?v=DinrKHKYFXY  

Answer 2

Option C is not logically valid

 

Comments

ramcharantej_24

sorry for late reply. I do not know which property but I am telling what am I thinking.

if p1.p2=true then p1+p2 will definitely be true so w(p1+p2)  will depend upon value of w so we can write

p1p2 + w + w(p1+p2) = p1p2+ w

Here w is main factor if w is false then w(p1p2) will be false. But if w is true then value of w(p1+p2) still be redundant because in both equation there is w with ORing condition so overall value would be true.

---

Navneet Singh Tomar you are proving B->A false by making T->F.that’s perfectly OK.But here we’ve to prove A->B false.we can do that by making T->F but that’s can’t be done here.

If B->A is false then how can u say A->B is false ??

---

@mrinmoyh Bro to prove logically valid both sides should be true that is A->B as well as B->A should be true.

A->B= True

B->A= False

So overall it is false hence not logically valid

Answer 3

Option A and B are pretty clear. They are logically valid.

Option C and D can be checked with a simple truth table construction taking two values x1 and x2, i.e. p(x1) and p(x2)

Note:-

Column 3 below indicates L.H.S of option C.

Column 4 below indicates L.H.S of option D.

Column 5 below indicates R.H.S of option C and D.

p(x1)	p(x2)	(p(x1)->W) $\Lambda$ (p(x2)->W)	(p(x1)->W) $\vee$ (p(x2)->W)	(p(x1) $\Lambda$ p(x2))->W
T	T	W	W	W
T	F	W	T	T
F	T	W	T	T
F	F	T	T	T

 

You can clearly see the 3rd column is not matching with the 5th column.  So option C is not valid which is the required answer.

Answer 4

Laws for Manipulating Quantifiers: There is rule analogous to DeMorgan's law that allows us to move a NOT operator through an expression containing a quantifier.

• $\neg (\forall x\: P(x)) \equiv \neg \forall x \neg P(x) \equiv \exists x \neg P(x)$
• $\neg (\exists x\: P(x)) \equiv \neg \exists x \neg P(x) \equiv \forall x \neg P(x)$

Domain $: p_{1},p_{2}$

A.$\forall x (p(x)\vee W)\equiv \forall x\:p(x) \vee W$

$\textsf{LHS}:\forall x (p(x)\vee W) \equiv \forall x \:p(x)\vee W \equiv p_{1}p_{2}+W$

$\textsf{RHS}:\forall x \:p(x)\vee W \equiv p_{1}p_{2}+W$

Here, $\textsf{LHS} = \textsf{RHS}$

So, option $(A)$ is Valid.

B.$\exists x (p(x)\wedge W)\equiv \exists  x\:p(x) \wedge W$

$\textsf{LHS}:\exists x (p(x)\wedge W) \equiv (p_{1} + p_{2})\cdot W $

$\textsf{RHS}:\exists  x\:p(x) \wedge W \equiv (p_{1} + p_{2})\cdot W $

Here, $\textsf{LHS} = \textsf{RHS}$

So, option $(B)$ is Valid.

C.$\forall x (p(x)\rightarrow W)\equiv \forall x\:p(x) \rightarrow W$

$\textsf{LHS}:\forall x (p(x)\rightarrow W) \equiv \forall x(\neg p(x) \vee W) \equiv \forall x\:\neg p(x)  \vee W \equiv \overline{p_{1}}\overline{p_{2}} + W \equiv \overline{(p_{1} + p_{2})} + W$

$\textsf{RHS}:\forall x\:p(x) \rightarrow W \equiv \neg [\forall x\: p(x)] \vee W = \neg \forall x \neg p(x) \vee W \equiv \exists x \neg p(x)\vee W \equiv \overline{p_{1}} + \overline{{p_{2}}} + W \equiv \overline{(p_{1}\cdot p_{2})}+ W$

Here, $\textsf{LHS} \neq  \textsf{RHS}$

So, option $(C)$ is NOT Valid.

D.$\exists x (p(x)\rightarrow W)\equiv \forall x\:p(x) \rightarrow W$

$\textsf{LHS}:\exists x (p(x)\rightarrow W) \equiv \exists x (\neg p(x)\vee W) \equiv \exists x \neg p(x)\vee W \equiv \overline{p_{1}} + \overline{p_{2}} + W$

$\textsf{RHS}:\forall x\:p(x) \rightarrow W \equiv \neg (\forall x\: p(x)) \vee W \equiv \neg \forall x \neg p(x) \vee W \equiv \exists x \neg p(x) \vee W \equiv \overline{p_{1}} + \overline{p_{2}} + W$

Here, $\textsf{LHS} = \textsf{RHS}$

So, option $(D)$ is Valid.

So, the correct answer is $(C).$

Comments

see i totally understand how and what you are trying to prove, but i have a doubt

 

in explanation of option c you took for-all and distributed it within the bracket after converting implies to boolean logic

and according to distributive law

→ for-all is distributive over conjunction, not disjunction

→ there-exists is distributive over disjunction, not conjunction

 

it can be either of two cases

case 1 ) → as w has no free occurrence of x so it becomes constant and then for-all is able to distribute over disjunction

or

case 2 ) → i missed something, i would appreciate if you could solve my doubt