GATE CSE 2004 | Question: 81

Question

Let $G_1=(V,E_1)$ and $G_2 =(V,E_2)$ be connected graphs on the same vertex set $V$ with more than two vertices. If $G_1 \cap G_2= (V,E_1\cap E_2)$  is not a connected graph, then the graph $G_1\cup G_2=(V,E_1\cup E_2)$

• A. cannot have a cut vertex
• B. must have a cycle
• C. must have a cut-edge (bridge)
• D. has chromatic number strictly greater than those of $G_1$ and $G_2$

Comments

G1∩G2=(V,E1∩E2)  is not a connected graph,

wht does it mean

---

Why we are not taking directed graph here? Will there also be a cycle then?

---

Proof G1 U G2 has cycle

credits:- https://stackoverflow.com/a/50458578
 

Answer 1

Take a tree for example 

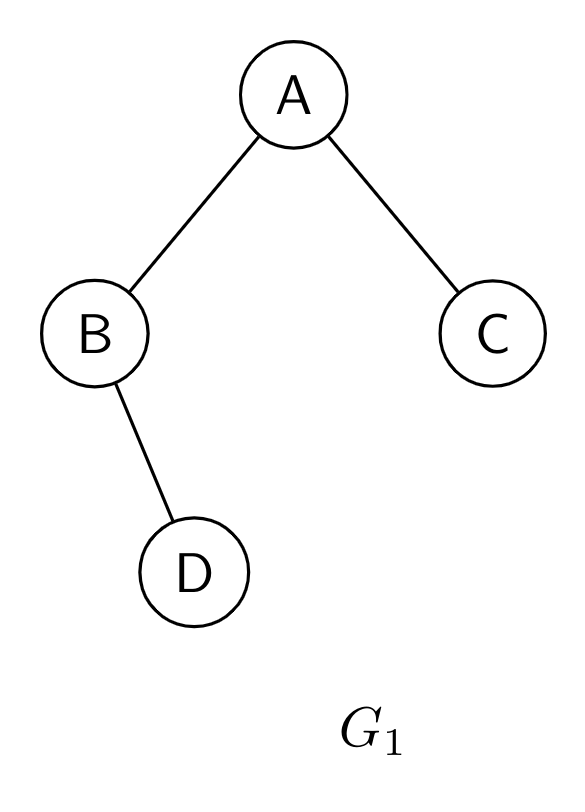
• A. False. Every vertex of tree (other than leaves) is a cut vertex.
• B. True.
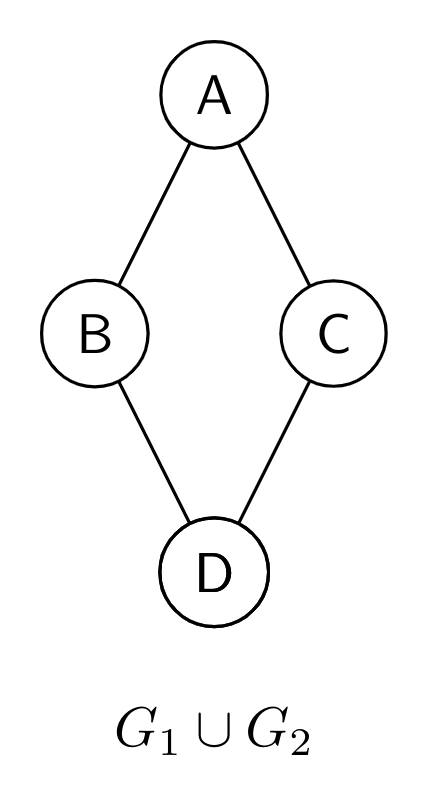
• C. False. There is no cut-edge (an edge whose removal increases the number of connected components in  graph) in $G_1 \cup G_2.$
• D. False. $G_1 \cup G_2$, $G_1$ and $G_2-$ all three graphs have same the chromatic number of $2$. 

Now, we have given counter examples for options A,C and D. So, option B is the only possible answer and its proof is given at end.

Correct Answer: Option B

---

We are given that $G_1$ and $G_2$ are connected. So, if we take any two vertices say $v_i$ and $v_j$ there must be path between them in both $G_1$ and $G_2.$ Now, it is given that $G_1\cap G_2$ is disconnected. That is, we have at least two vertices $v_1$ and $v_2$ such that there is no path between them in $G_1 \cap G_2.$

This means the path between $v_1$ and $v_2$ in $G_1$ and $G_2$ are distinct. 

When we have two distinct paths between a pair of vertices in a graph, it forms a cycle.

Comments

G1 and G2 are connected graph. As G1 $\cap$ G2 is disconnected graph, there must exist two vertices say V1 and V2 such that there is no path between them in G1 $\cap$ G2.

But as G1 is connected graph it must have some path P1 between vertices V1 and V2. Similarly, G2 must have some path P2 between V1 and V2.

Now, these P1 and P2 are not the same paths, if they are they will be present in G1 $\cap$ G2, which will contradict with our assumption.

In G1 $\cup$ G2, we have two paths P1 and P2 to between V1 and V2. That form the cycle. See the image.

---

@srestha but G1 intersection G2 is connected but should be not connected as specified in question.

Correct me if m wrong.

---

@Prateek

See the node D, if you try to take intersection of G1 and G2, D will be disconnected as the path is not common in G1 and G2.

---

@srestha

G1 intersection G2 is disconnected or not?

I found that we have a common path in both G1 and G2 ,which is connected.

what actually G1 and G2 intersection is?

---

in question they said consider more then 2 vertices !

---

@srestha

your 1^st option explanation does not follow the question, you said G1 and G2 is tree so it must have a cut vertex but it was talking about (G1 intersect G2) which does not have any cut vertex in your given example...

---

Great explaination!

---

Here, vertex named 2 is the cut vertex in (G1 U G2 ).Look at the diagram below.

---

if the graph is weakly connected directed graph then there may not be cycle..

If graph is strongly connected .

Cycle exist ,no cut vertexe, no cut edge ...

---

@Subbu. do you have any reference to support your statement.

---

here G1 U G2 does not have a cut vertex in this example, am i correct?

Answer 2

Say G1 is Black colored graph, and G2 is red colored graph.
In this figure i overlapped both graphs, to see them together.


Given that $G_1 \cap G_2 $ is Disconnected, To make it happen G1 and G2 has to meet somewhere and then leave at some point, Once they leave each other and then have to meet somewhere again to have atleast two different disconnected component.
Now it is clear that this will form a cycle (See image has cycle.)

Note: If  $G_1 \cap G_2 $ need not to be disconnected then $G_1\cup G_2 $ need not to have a cycle.

(in this case when one of the Graph has cycles then only $G_1\cup G_2$ can have cycle.)

Comments

amazing explanation!!

---

Note: If (G1 intersection G2 )need not to be  disconnected then G1UG2 need not to have a cycle…

This statement true only if both edge sets are same … E1=E2 then only G1U G2 doesn't contain cycle.…

Answer 3

A very simple reasoning in this question may fetch the answer very fast. Since the two graphs G1 and G2 are connected, there will be path from a vertex to every other vertex in  both G1 and G2 but since G1 ∩ G2 is not connected , at least for one vertex pair v1,v2 the connecting paths must be different in both G1 and G2. Hence G1 union G2 will definitely have a cycle.

Answer 4

There would be "at least " one cycle there in G1 Union G2

Comments

you should also proof ,do they have cut vertex??,i think no by seeing your examples