GATE CSE 2005 | Question: 82a

Question

Let $s$ and $t$ be two vertices in a undirected graph $G=(V,E)$ having distinct positive edge weights. Let $[X,Y]$ be a partition of $V$ such that $s \in X$ and $t \in Y$. Consider the edge $e$ having the minimum  weight amongst all those edges that have one vertex in $X$ and one vertex in $Y$.

The edge $e$ must definitely belong to:

• A. the minimum weighted spanning tree of $G$

• B. the weighted shortest path from $s$ to $t$

• C. each path from $s$ to $t$

• D. the weighted longest path from $s$ to $t$

Comments

The answer is A. We can prove this by a simple contradiction proof.

Suppose the given edge was not part of the minimum spanning tree. Now, since the minimum spanning tree is connected by definition, there exists another path from X to Y and another edge which crosses from set X to set Y which makes this path possible. But, this path's length has to be strictly greater than the previous one because the original edge, by definition, was the minimum. So any MST which doesn't contain that edge will not be minimum.

---

Every light edge which crosses the cut will defenitely be present in the minimum spanning tree.(Refer Cormen exercise 23.1-6)….Therefore we can parition in such a way that there is cut present and e crosses it.also s on one side and t on other side.…..Hope it helps..

Light edge means the edge with least weight that crosses the cut….

---

If a Graph have a Unique MST then the edges of that Spanning tree is lightest weighted edge on some Cut , not every cut.

Answer 1

The answer should be Option A because edge $e$ is the lightest safe edge connecting $X$ and $Y$ so the minimum spanning tree of $G$ must contain $e$ (Greedy and optimal choice).
While option $(B)$ might seem correct but it is not always true. One such case is when $G$ is not connected therefore there might not be any path between $s$ and $t$.
Since the question is about definitely TRUE, $(B)$ is incorrect and $(A)$ is the only correct option

Lets say $AC =1$, $CD = 2$ ,$BD = 3$ and  $AB=4$

Then if  $s= A$  and  $t= B$ then $AC$  is the lightest edge crossing $X$ and $Y$ where  $X = { A }$  and $Y = { C, B, D}$
But clearly $AC$ is not on the shortest path from $A$ to $B$. The shortest path is $AB = 4$.

Comments

Partitions will always be bipartite or not?

---

 

one vertex in X and one vertex in Y.

What does this mean?

---

neel19 the minimum edge e has one node in X and one node in Y.

Answer 2

Answer for 82 b) is option a) A path from s to t in MST.

T is the spanning tree and E_T is the edge set of the tree.

Let L denote the set of all paths P_e in T where e is any edge in E_G. For g ∈ E_T , we define the congestion of g as the number of paths in L in which g is an element:

c(g, T) = |{P_e ∈ L : g ∈ P_e}|. 

We then define the congestion of G embedded onto T as the maximum c(g, T) over all edges g in E_T :

c(G : T) = max{c(g, T) : g ∈ E_T }. 

The tree congestion of G, denoted t(G), is the minimum value of c(G : T) over all trees T in T_G. Similarly, the spanning tree congestion of G, denoted s(G), is the minimum value of c(G : T) over all spanning trees S in S_G:

t(G) = min{c(G : T) : T ∈ T_G},

s(G) = min{c(G : S) : S ∈ S_G}

Please refer to the link 

http://www.math.csusb.edu/reu/dt07.pdf

Comments

could someone explain this in an easier way?

---

I think answer to B part is option B.

(A)----5---(B)----5---(C)
 |                     |
 |----------7----------|

So in this example, A-C Shortest path is 7. But that will not be the path included in minimum spanning tree. Because spanning tree would be A->B->C

---

Yes you are true but acc. to question congestion (ato c ) is max  weight among  edges lies from a to c. Therefore for a to c in MST  congestion=5.

From a to c in weighted shortest path congestion = 7.

But you may be true in some cases when direct path is less than MST

Answer 3

The minimum weight edge on any s-t cut is always part of MST. This is called Cut Property. This is the idea used in Prim's algorithm. The minimum weight cut edge is always a minimum spanning tree edge. Why B (the weighted shortest path from s to t) is not an answer? See below example, edge 4 (lightest in highlighted red cut from s to t) is not part of shortest path. 

Comments

Shouldn't minimum weight edge 'e' be directly connected to s and t? As mentioned in the question that 'e' is minimum among those edges that have one vertex in X and another vertex in Y. Please feel free to correct me if I am wrong.

Answer 4

 

Option: (A) the minimum weighted spanning tree of G

Consider the following graph-

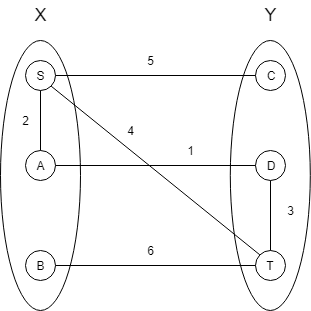
Here, (A, D) is the edge e with weight 1.

The shortest path S to T is (S, T) which does not contain e. Therefore, option (B) is false.

Also, we can see that e is not part of every path from S to T. Therefore, option (C) is false.

Similarly, we show that there can be certain graphs where e is part of the shortest path from S to T.

However, we can see that e is the edge with the minimum weight that connects the vertex set X to vertex set Y, therefore, it must always be present in the MST.

Therefore, the correct option is (A).

Comments

@Debargha Bhattacharj

AD is nothing but another name of ST according to question. Isnot it??

Actually among option A) and B) both could be true.

But A) is more meaningful and logical than B).

So, A) is best choice. rt??

---

@srestha

AD is nothing but another name of ST according to question. Isnot it??

I don't think so. Actually, s and t are two specific vertices in the vertex sets X and Y respectively, which, in the figure, I have mistakenly represented using equivalent uppercase letters.

Now, it is mentioned in the question that among all the edges that connect some vertex in X to some other vertex in Y, e is the edge having the minimum weight. In the above example, e is actually the edge AD with weight 1. 

Now, using the example of the above graph, we can eliminate option (B), (C) and (D).

---

yes, right.