TIFR CSE 2012 | Part A | Question: 15

Question

Consider the differential equation $dx/dt= \left(1 - x\right)\left(2 - x\right)\left(3 - x\right)$. Which of its equilibria is unstable?

• A. $x=0$
• B. $x=1$
• C. $x=2$
• D. $x=3$
• E. None of the above

Answer 1

Here, $dx/dt$ is neither constant nor function of variable $t.$ So, on solving for $x,$ we get exponential decay function something similar to radioactive decay $dN/dt = -KN ;K>0.$

For any  equilibrium point, we have $dx/dt = 0 \implies x = 1,2,3.$

Now if we consider sign scheme of $dx/dt$ for different ranges of $x,$ we have :

• $dx/dt > 0$ for $x < 1;$
• $dx/dt  < 0$ for $1 < x < 2;$
• $dx/dt  > 0$ for $2 < x < 3;$
• $dx/dt  < 0$ for  $x > 3;$

For $x \to 2, dx/dt$ changes from negative to positive. So, $x = 2$ is a point of unstable equilibrium.

Since, here $dx/dt$ is a function of $x$ not $t,$ so condition for checking stable / unstable points (aka local minima / local maxima) is opposite to what we apply in case of $dy/dx = f(x).$ Here we have $dy/dx = f(y)$ which is actually exponential function in $y$ and $x.$

We can understand equilibrium in terms of radioactive decay.

Let $dN/dt = -KN ;K>0$ its significance is that an element is loosing energy so it is getting stability because we know more energy an element gets,more de-stability it gains and vice versa.

Correct Answer: $C$

Comments

Hello shashank

from where you studied this ?

because as per my knowledge both your answer and concept behind answer is wrong.

Tell me if i'm missing something.

---

@shashank mind blowing explanation

---

@Shashank Kumar could you please explain what happens at points x=1 and x=3. Also why are they not considered unstable?

Answer 2

Equilibrium points for any curve y=f(x)

points where $\frac{\mathrm{d}y}{\mathrm{d} x}=0$ (which is a function of y) are called Equilibrium points.

// y'=f(y)=0

Now Equilibrium points can be of two types

1) Stable :- from stable points if we move little bit right or left , in both cases we will come closer to equilibrium. in more simple words you can think like some ⋃ kind bowl , in which you places some glass pebbles , then you can think they will always reach to equilibrium so thins is stable point of equilibrium.

Mathematically stable points are those where $\frac{\mathrm{d} y}{\mathrm{d} x}$ would be -ve if you move bit right from point of equilibrium and $\frac{\mathrm{d} y}{\mathrm{d} x}$ would be +ve if you move bith left from the point of equilibrium.

2) Unstable :-From unstable points if we move lil bit right or left , we're going away from equilibrium in both cases.Now think any bowl of shape ⋂ , place any glass pebble , it will always move away from equilibrium so this is unstable point fo equilibrium.Mathematically unstable points are those where $\frac{\mathrm{d} y}{\mathrm{d} x}$ would be +ve if you move bit right from point of equilibrium and $\frac{\mathrm{d} y}{\mathrm{d} x}$ would be -ve if you move bith left from the point of equilibrium.

Now from this theory we can easily see x=2 is an unstable point of equilibrium while x=1 and x=3 are both stable points of equilibrium.

Comments

Hi Rupendra,

In nutshell, If we consider sign of dy/dx w.r.t to 'x', dy/dx is -ve on left & +ve on right for the equilibrium point i.e. we get minima at the point which becomes stable point because graph of y = f(x) becomes decreasing on LHS  & increasing on RHS of equilibrium point.

Now if we consider say dy/dx w.r.t. to 'y', things get reversed because entire curves get reversed because of change in axis. So we can say what was earlier minima is now actually maxima and hence becomes unstable point.

---

Hello Shashank

I respect your time Shashank.If you think it's trivial question which i'm taking too long to understand , you can ignore this. But i really didn't understand your maxima/minima point.

Let suppose $y=x^2$ then $\frac{\mathrm{d} y}{\mathrm{d} x}$=$2x$

Now as we're interested in such a $\frac{\mathrm{d} y}{\mathrm{d} x}$ which is a function of $y$ so lets make it.

$\frac{\mathrm{d} y}{\mathrm{d} x}$= $2 x$ =$2 \sqrt{y}$

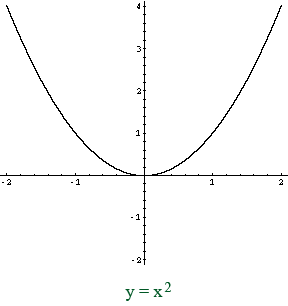
It's graph of $y=x^2$ which have global minima at $x=0$

Now below curve is of $\frac{\mathrm{d} y}{\mathrm{d} x}$ vs $y$

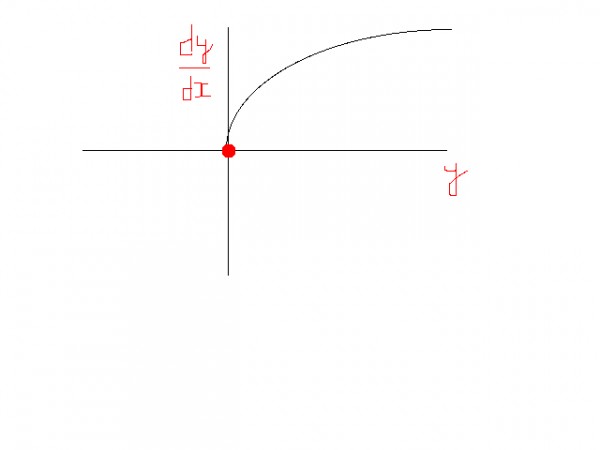
Still i don't know how minima became maxima.

I played lil bit with our original differential equation and got relation b/w x and y

$\int \frac{dy}{(1-y)(2-y)(3-y)} =\int dx$

$\int ( \frac{1}{2(1-y)}-\frac{1}{2-y}+\frac{1}{2(3-y)})dy $

so x=ln$((2-y)*\sqrt{\frac{3-y}{1-y}})$

now even this baffled me more. this says x is not define at y>=1

if i study $\frac{dy}{dx}$ curve then it says that at 2⁺ dy/dx=+ve and at 2^- it's -ve and this is exactly what we use for minima.if we go bit right of minima point then dy/dx slop will increase and if we go bit left , slope will fo on decreasing...

---

@Rupendra Choudhary, i think you messed up with logic of maxima and minima.. if in U shape from bottom most point if you move little further right then dy/dx will be +ive  i.e means local minima which you explained opposite in you answer.