Considering when $k=3$
$T(n)=T(\frac{n}{3})+T(\frac{3}{4})+n$
Below is the recursion tree
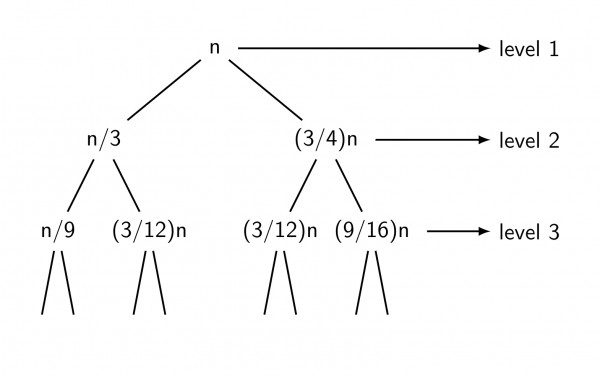
Since, the combine work according to recurrence is linear in term of the size of the sub-problem
so at Level 1, total combine work is $n$
Combined work at level 2$=\frac{n}{3}+\frac{3n}{4}=\frac{13n}{12}$
At level 3 combine work $=\frac{n}{9}+\frac{3n}{12}+\frac{3n}{12}+\frac{9n}{16}=(\frac{13}{12})^2n$
So, at level $k$, when the recursion bottoms out at $T(1),$ the combine work will be $(\frac{13}{12})^{k-1}.n$
The left height of the tree is when the subproblem $\frac{n}{3}$ would bottom out and that is when $\frac{n}{3^k}=1$
gives $k=\log_3n$
The right height of the tree is $\log_{\frac{4}{3}}n$
for the purpose of upper bound consider right height and then sum up total combine work from root till the leaf level
$n+\frac{13}{12}n+(\frac{13}{12})^2.n+\ldots+(\frac{13}{12})^{\log_{\frac{4}{3}}n-1}n$
$=n\left [ 1+\frac{13}{12}+\ldots +(\frac{13}{12})^{\log_{\frac{4}{3}}n-1} \right ]$
$=n \left[ 1.\frac{(\frac{13}{12})^{\log_{\frac{4}{3}}n}-1}{\frac{13}{12}-1} \right]$
Using property
$a^{\log_bc}=c^{\log_ba}$
and ignoring denominator as constant term for upper bound
$n.\left [ n^{\log_{\frac{4}{3}}\frac{13}{12}} -1\right ]=n^{1.27}$ (approximately)
Option (A) : $O(n^{1.5})$ is surely an upper bound when k=3. Correct option.
Option (B): $O(n\log n)$
this means $n.n^{0.27} \leq c.n.\log n$
$n^{0.27}\leq c.\log n$
This is clearly false as polynomials grow faster than poly-logarithms.
Option(B) can never be an upper bound, yes lower bound possible when $k=3.$
When $k=4.$
$T(n)=T(\frac{n}{4})+T(\frac{3n}{4})+n$
If we draw recursion tree for this, at every level cost comes to be n and there would be maximum $\log_{\frac{4}{3}}n$ levels
So, in this case $T(n)=O(n\log n)$. Option (C) correct.
When $k=5,$
$T(n)=T(\frac{n}{5})+T(\frac{3n}{4})+n$
It's recursion tree would look like below:
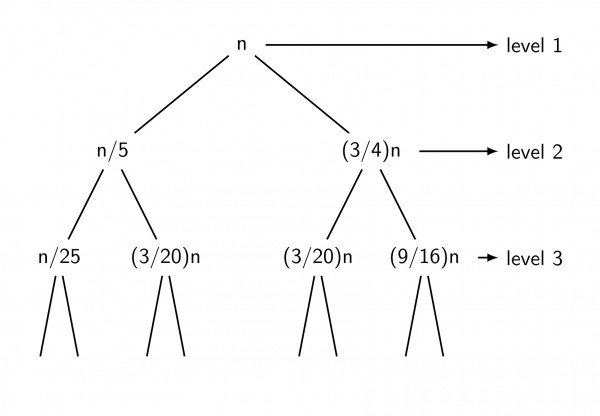
Level 1 Total cost $=n$
Level 2 total cost $=\frac{19n}{20}$
Level 3 total cost $=(\frac{19}{20})^2.n$
Level k cost $=(\frac{19}{20})^{k-1}.n$
Number of levels on right $=\log_{\frac{4}{3}}n$
Number of levels on left $=\log_5n$
For the purpose of upper bound I'll consider right height.
Computing total cost from root till leaf
$n.\left[1+\frac{19}{20}+\ldots +(\frac{19}{20})^{\log_{\frac{4}{3}}n-1} \right]$
$=n.\left[ \frac{1-(\frac{19}{20})^{\log_{\frac{4}{3}}n}}{1-\frac{19}{20}}\right]$
Ignoring denominator as we are only interested in some function of $n.$
$=n.\left[ 1-(\frac{19}{20})^{\log_{\frac{4}{3}}n} \right]$
$=n\left[1-n^{\log_{\frac{4}{3}}\frac{19}{20}} \right]$
$=n[1-n^{-0.17}]$
$=n-n^{0.82}$
So, option(E) is correct.
Option(D) which says $O(n\log n)$ might not look convincing but
$n-n^{0.82} \leq c.n\log n$
$1-\frac{1}{n^{0.17}} \leq c\log n$
for $c=1,n_o=2$ this satisfies big-oh.
Option (D) is also correct.
Answer: option(B)