MadeEasy Test Series: Algorithms - Minimum Spanning Trees

Question

Comments

AB=1;AC=2;BC=3;BD=4;AD=5;CD=6;DE=7;AE=8;BE=9

MST of a graph with 5 vertices will have 4 edges {AB,AC,BD,DE}. Weight=1+2+4+7=14

Is it okay now?

---

@mitesh kumar

Try to apply kruskal,

Sum=0

(AB)Edge 1, no other choice, sum = 1

(BD)Edge 2, no other choice, sum = 1+2

(AD)Edge 3 can be avoided if you assign it such that it results in a cycle 

(DE)Edge 4, no other choice, sum = 1+2+4

(BE)Edge 5 can be avoided if you assign it such that it results in a cycle

(AE)Edge 6 can be avoided if you assign it such that it results in a cycle

(EC)Edge 7, no other choice, sum = 1+2+4+7

Weight of MST= 14

Please mention the name of test series in title.

---

Ans  given is 14

---

I edited it.. please check

---

@MiNiPanda  yes ans  is correct but

Is there any specific approach or simple permutation?

---

Try to eliminate the edges. Suppose we allocate AB = 1, followed by AC=2, Now allocate BC=3. So once we select AB, AC through krushkal algorithm, we cant select BC because that would form a chain. So in that case BC (weight = 3) is eliminated. Proceed with the similar approach, we will get 14 as the minimum spanning tree with maximum weight.

---

@mitesh kumar

nothing as such..keep assigning smaller weights to edges forming cycle so that these weights have to be discarded from MST.

In a simple undirected graph at least 3 edges have to be there to form a cycle.

Since two edges can't form a cycle so the smallest 2 weights i.e. 1 and 2 have to be included whichever edge you assign these weights to.

Now the 3rd smallest i.e. 3 is assigned to BC purposefully so that a cycle ABC is formed with edge 1 and 2 and it has to be rejected.

In this way we always should try to search for cycles and assign smaller weights for such problems.

Answer 1

The answer should be $14$

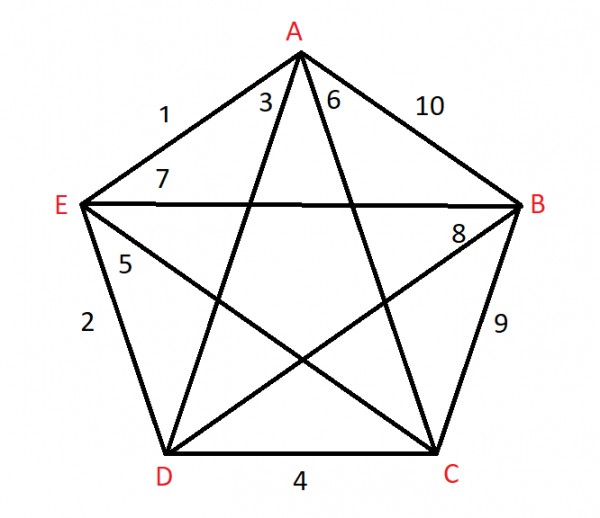
The edges in increasing order are

$\left \{ AE=1,ED=2,AD=3,DC=4,EC=5,AC=6,EB=7,DB=8,BC=9,AB=10 \right \}$

Applying Kruskal's algorithm:

We take $AE,ED$, we will not take $AD$ as $A$ and $D$ are already covered, then $DC$, then we will not take $EC$ and $AC$, then we will take $EB$

Edges in minimum spanning tree are : $\left \{ AE,ED,DC,EB \right \}$

Weight of minimum spanning tree = $1+2+4+7=14$