Here first both $|x|,|y|\leq 1$ as otherwise both A and B will have values greater than 1 hence would not satisfy the inequality.
Now, Let $(x,y)\in A$ then $x^2+y^4 \leq 1$
$\Rightarrow$ $x^4+y^6 = x^2 *x^2 +y^2*y^4 \leq 1^2 *x^2 +1^2*y^4 = x^2 + y^4 \leq 1$
$\Rightarrow$ $x^4+y^6 \leq 1$
Thus $(x,y)\in B$
Hence every point in A is also in B or $A \subseteq B$.
We can also prove the above by,
$x^4 \leq x^2$ since $|x|\leq 1$ , similarly $y^6\leq y^4$ as $|y|\leq 1$ ,
$\Rightarrow$ $x^4+y^6 \leq 1$.
Now since $x^4+y^6<x^2+y^4 \leq 1$ there exists a point $(x_1,y_1)$ such that $|x_1|,|y_1| \leq 1$
for which the value of $x_1^4+y_1^6<1$
but $x_1^2+y_1^4>1$ ,
hence $B\not\subset A$ $\Rightarrow$ $B \neq A$.
This point $(x_1,y_1)$ must be along the boundaries as can be seen from the below image that as the value of the equations in A and B both increases value with increase in the value of $(x,y)$ due to even powers.
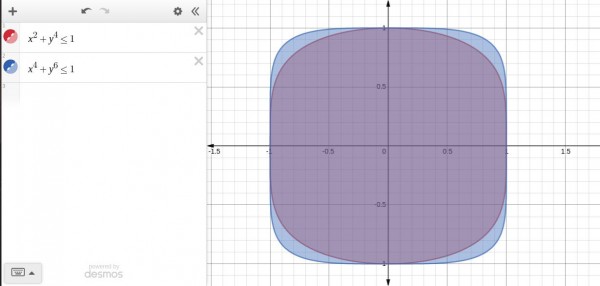
Thus the answer is Option (B)