Memory Based GATE DA 2024 | Question: 13

Answer 1

Answer: 6

let Expected number of throws be $ E[X]$

$E[X] = \sum E[x_{i}] * P_{i}$

$E[X] = $ (case when first output  = 2 or 4 or 6) + (case when first output  = 1 or 3 or 5)

$E[X] = $  (case when first output  = 2 or 4 or 6) *(case when second output = 2 or 4 or 6)
               +  (case when first output  = 2 or 4 or 6)* (case when second output = 1 or 3 or 5)  
               + (case when first output  = 1 or 3 or 5)

reference image :


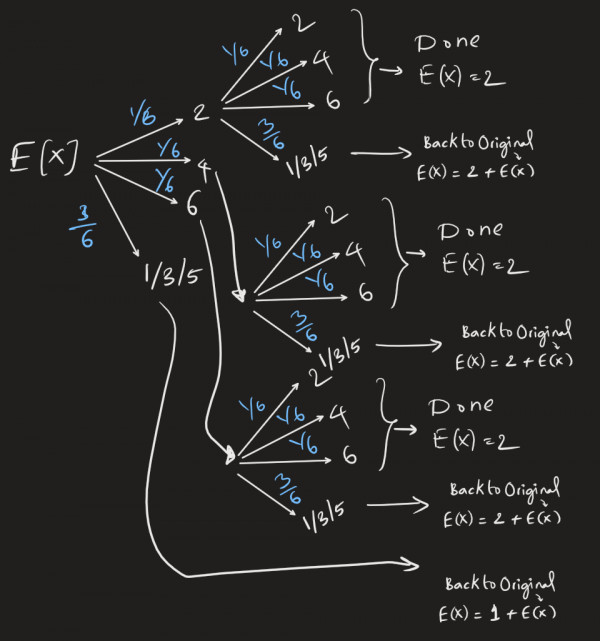
writing it as recursive equation , since we are back to original state (back to starting state)

i.e, say after k trails

    $E[X_{i}] = P_{i} * (k + E[X])$


solving the equation:

$E[X] = $$3*(2 * \frac{1}{6} * \frac{3}{6})$ + $3*((2 + E[X] )* \frac{1}{6} * \frac{3}{6})$ +  $((1 + E[X] )* \frac{3}{6} )$ 

$E[X] = $$\frac{6 * 3}{6 * 6}$ + $((2 + E[X] )* \frac{3*3}{6*6})$ +  $((1 + E[X] )* \frac{3}{6} )$ 

$E[X] = $$\frac{1}{2}$ + $((2 + E[X] )* \frac{1}{4})$ +  $((1 + E[X] )* \frac{1}{2} )$ 

$E[X] = $$\frac{2}{4}$ + $((2 + E[X] )* \frac{1}{4})$ +  $((1 + E[X] )* \frac{2}{4} )$ 
 

4* $E[X] = $ $2 + (2+ E[X] ) + 2*(1+ E[X])$

4* $E[X] = $ $2 + 2+ E[X]  + 2+ 2E[X]$

we get, $E[X]$ = expected number of throws = $6$ 

Answer 2

This can be solved recursively. E(X) = E = (1/2)(1+E) + (1/2)(1+(1/2)(1) + (1/2)(1+E)).

Solve this for E and you will get the answer as 6.