GATE CSE 1998 | Question: 4

Question

Design a deterministic finite state automaton (using minimum number of states) that recognizes the following language:

$L=\{w \in  \{0, 1\}^* \mid w$  interpreted as binary number (ignoring the leading zeros) is divisible by five $\}.$

Comments

 @Verma Ashish  +1 for the links!

---

For Decimal ( Binary String ) = 0 mod n

  i)   If n = $2^m$, then No.of states in Minimal DFA = m + 1 (Proof given by arjun sir in this question)

 ii)   If  n = odd, then No.of states in Minimal DFA = n

iii)   If n = even but not power of 2, then follow division technique until your value matched with case i or  case ii

For example,

If n=21 ===> then No.of states in Minimal DFA = 21

If n=32 ===> then No.of states in Minimal DFA = 6

If n=22 ===> then No.of states in Minimal DFA = 12 due to

( $\frac{22}{2}$→ one time division → 11 → is odd ) ===> 1+ 11

If n=12 ===> then No.of states in Minimal DFA = 5 due to

( $\frac{12}{2}$ → $\frac{6}{2}$ → two time division → 3  →  is odd )

===> 2 + 3

Source: https://gateoverflow.in/272643/cant-understand-the-intution-behind-the-shortcut

---

When the initial state is the final state, then epsilon also gets accepted. So, according to this question, what decimal number is epsilon supposed to represent? Is epsilon representing binary / decimal 0 here?

Answer 1

Suppose we have decimal no $3$ after that we get a symbol $2$ . it becomes $32$ as  $3 x 10 +2 = 32 $

In binary if we have $10$ ( i.e $2$ in decimal say old no) and after that we get symbol $1$ it become $101$( i.e $5$ in decimal say new no ) 

$ 2$ (old no.) $ \times 2$( base)  $+1$( input symbol) $= 5$ (new no.)

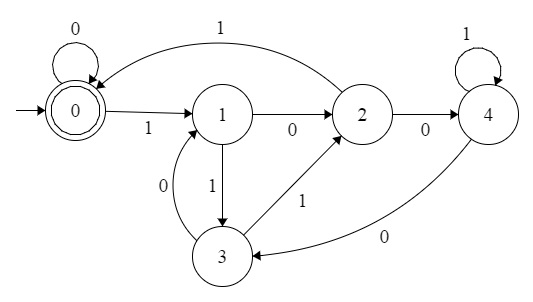
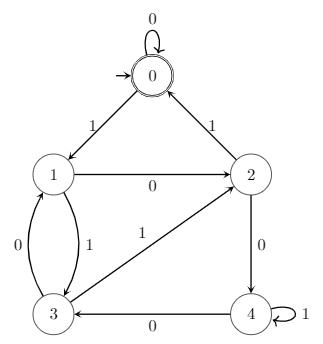
Now in the given problem, binary no is divisible by $5$ , i.e $0,101,1010,1111..... $

We need $5$ states in DFA , $0,1,2,3$ and $4$ .Each state represent remainder that comes when we divide no by $5$.

Input symbol $=\{0,1\}$

We get the transition:

[Old state $\times$ base $+$ input symbol] mod $5 =$ New state    , where base is $2$ 

$[0 \times 2 + 0]mod \ 5 = 0$           $[1  \times 2 + 0]mod \ 5 = 2$         $[2  \times 2 + 0]mod \ 5 = 4$       

$[0 \times 2 + 1]mod  \ 5 = 1$           $[1  \times 2 + 1]mod \ 5 = 3$         $[2  \times 2 + 1]mod \ 5 = 0$       

$[3  \times 2 + 0]mod \ 5 = 1$           $[4  \times 2 + 0]mod \ 5 = 3$

$[3  \times 2 + 1]mod \ 5 = 2$           $[4  \times 2 + 1]mod \ 5 = 4 $

Comments

Minimal DFA that accept all Binary number's divisible by $5=5\ states$ 

	$0$	$1$
$q0$	$q0$	$q1$
$q1$	$q2$	$q3$
$q2$	$q4$	$q0$
$q3$	$q1$	$q2$
$q4$	$q3$	$q4$

---

DFAs drawn with this technique will be minimized DFA only when there is no common factor between number n and base b, e.g. between 5 and 2, or between 5 and 3.

Like for example in binary numbers, if the divisor is a power of 2 (i.e. 2^n) then the minimum number of states required will be n+1. How would you design such an automaton? Just see the properties of binary numbers. For a number, say 8 (which is 2^3), all its multiples will have the last 3 bits as 0. For example, 40 in binary is 101000. Therefore for a language to accept any number divisible by 8 we just need an automaton which sees if the last 3 bits are 0, which we can do in just 4 states instead of 8 states. That's half the complexity of the machine.

In fact, this can be extended to any base. For a ternary base number system, if for example we need to design an automaton for divisibility with 9, we just need to see if the last 2 numbers of the input are 0. Which can again be done in just 3 states.

So for any odd number n in a binary system, we need n states to define the language which accepts all multiples of n. On the other hand, if the number is even but not a power of 2 (only in case of binary numbers) then we need to divide the number by 2 till we get an odd number and then we can find the minimum number of states by adding the odd number produced and the number of times we divided by 2.

For example, if we need to find the minimum number of states of a DFA which accepts all binary numbers divisible by 20, we do :

20/2 = 10 
10/2 = 5

Hence our answer is 5 + 1 + 1 = 7. (The 1 + 1 because we divided the number 20 twice).

Source:

https://stackoverflow.com/a/33575441/631823

https://stackoverflow.com/questions/21897554/design-dfa-accepting-binary-strings-divisible-by-a-number-n#

---

Great explanation!! Thank you!

Answer 2

Ans...

here q0 is the initial state and final state

Comments

https://www.youtube.com/watch?v=UWrhRBfF6vM will help in better understanding above described method...........