GATE IT 2007 | Question: 50

Question

Consider the following finite automata $P$ and $Q$ over the alphabet $\{a, b, c\}$. The start states are indicated by a double arrow and final states are indicated by a double circle. Let the languages recognized by them be denoted by $L(P)$ and $L(Q)$ respectively.

The automation which recognizes the language $L(P) \cap L(Q)$ is :

• A.
• B.
• C.
• D.

Comments

$L(P)\cap L(Q)={\epsilon,a,b,aa,ab,b,aba,bab,aac,babab….\infty}$

• Option (B) $w=aa$ are accepted in the original but there is no path.
• Option (C) $w=aa,aac$ not path is define
• Option (D) $w=c$ is accepted but in the original DFA single $C$ is not accepted.

---

Option A is printed wrong in made easy pyqs book to anyone who's solving from there 🥲

---

Just Check abaac too.

Answer 1

Design an automaton using $P$ and $Q$  having $p_0q_0$ as start state  

$\delta(p_0q_0,a) \rightarrow \delta(p_0,a) \cup \delta(q_0,a)$
$$\begin{array}{|l|l|l|l|}\hline \text{Q \ $\Sigma$}  &  \text{a} & \text{b} & \text{c} \\\hline  \text{$\rightarrow p_0q_0^*$}  &  \text{$p_1q_2$} & \text{$p_2q_1$} & \text{} \\\hline 
\text{$p_1q_2^*$}  &  \text{$p_3q_3$} & \text{} \\\hline \text{$p_2q_1^*$}  &  \text{$p_1q_2$} & \text{$p_3$ (No Need)} & \text{}\\\hline \text{$p_3q_3^*$}  &  \text{} & \text{$q_2$ (No Need)} & \text{$p_2q_1$} \\\hline \end{array}$$

In case of intersection final states are those where final states of P and final states of Q come together. 

"No need" in above table mean, when we reach to $p_3$ (or $q_2$) then we cannot reach to any final state because we cannot have states of $P$ and $Q$ together (intersection). Hence, this is not shown in diagram [may draw a dead state for it to make it a DFA (as noted at end) ]

Automaton results in:

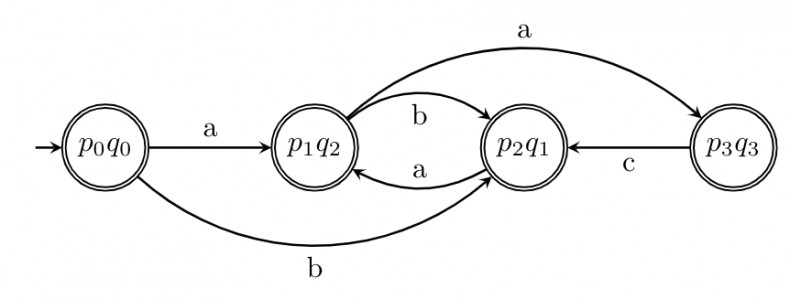
That is option A .

Note : DFA must have transition for each symbol $Q \times \Sigma \rightarrow Q$ and hence our automaton is not a DFA as we do not have transitions to dead state.

Comments

OR STRING 'BAA' IS COMMON TO ALL & OPTION 'A' CAN ONY GENERATE 'BAA'

---

can we only compare intial to intial , final to final state, and remaing all state to each other ?

---

Please explain the above mentioned table.

---

Design a DFA using P and Q  having p0q0 as start state  

where δ(p0q0,a) -> δ(p0,a)∪ δ(q0,a) = p1q2

---

Why you have not choosen all combinations possible like (p1,q1) or (p1,q3) like that ,can you please explain?

---

Because they are unreachable states ( we didn't get any transition to reach them)

---

@ Praveen i am not still able to understand it

---

great work praveen sir

---

I have a query sir.. As you have taken union for constructing the transition table for the intersection problem...

 

Do we need to take union for both type of questions (union and intersection) and construct the DFA ?

---

take the string "a_b_a_b_a_b_a_a_" you will see that only option a is accepting no other option, here in this question all state is final so don't think that every string will be accepted but at some state on seeing a or on seeing b, there is no movement.  

---

abaa string is common for both p and q. Now satisfy abaa for the options.. Only option a satisfies this.

---

A NOTE for students who are wondering “Can we apply Product Construction (Product Automata) on two NFAs ?”

The answer is YES.

We can apply Product construction on NFA , the Same way we do for DFA .. BECAUSE of the way product construction works..
If you know the proof and idea of “WHY” product construction works for DFAs and gives desired result, you will get to know that the same idea applies on NFAs too.

BUT for NFAs , the product automata might be MUCH bigger and messier than what we have for DFAs.
Also error prone if there are Epsilon transitions So needs a lot of care while doing it.

---

A simple solution to this question is that both automata of question accept string ‘aa’ but none of the options other A accept(others reject it) so, option A is correct answer.

Answer 2

See the languages being accepted by P and Q. In P before a 'c' there must be either 'b' or 'aa'. In Q, before 'c' there must be 'aa'. So, obviously, in their intersection before 'c' there must be 'aa' which is satisfied only by option A.

Comments

1. For finding such cases quickly, just check which transitions are absent from particular state and try to generate that string. If it is present in options, reject it,

2. Generate string like kleene closure in increasing order and check which is satisfied by question but not by options.

2 is always good approach.

---

edit : In P before a 'c' there must be either 'bb' or 'aa'

---

@mohan  In P before a 'c' there must be either 'b' or 'aa' because in string “bbcbc” before last c there is only b, not bb.

Answer 3

One string "aa" is common to both.
Which is accepted by only A not by any other machine. (Ans)

Comments

easiest among all answer.

---

string aa is not accepted by option (a) so answer will be option (e) none of the above.

---

@gdas Recheck your observation.

Answer 4

ans (A)...

Comments

don't you think brute force is risky as we may end up missing up a few strings and land upon an incorrect option?

---

What is mean by brute force method here ???

---

Trying random strings and check whether it satifies the option or not.