GATE CSE 2021 Set 2 | Question: 12

Question

Let $L_1$ be a regular language and $L_2$ be a context-free language. Which of the following languages is/are context-free?

• A. $L_1 \cap \overline{L_2} \\$
• B. $\overline{\overline{L_1} \cup \overline{L_2}} \\$
• C. $L_1 \cup (L_2 \cup \overline{L_2}) \\$
• D. $(L_1 \cap L_2) \cup (\overline{L_1} \cap L_2)$

Answer 1

Correct Answer: B,C,D

---

Some insights beforehand:

• CFLs are Not Closed under Intersection:
  $L_1=\{a^nb^*c^n\},L_2=\{a^nb^nc^*\}$ , $L_1\cap L_2=\{a^nb^nc^n\}$ not a CFL
• CFLs are Closed under Union:
  Let both of these CFLs be represented using grammars with start symbols $S_1$ and $S_2$ respectively. We define a new symbol $S^{’}$ such that $S^{’}\to S_1\mid S_2.$ Note: the resulting language may or may not be deterministic but will be context-free.
• CFLs are Not Closed under Complementation:
  $L_1\cap L_2=\overline{\overline{L_1}\cup\overline{L_2}}$
  We know that CFLs aren’t closed under intersection but is closed under union. So it must be the case that CFLs aren’t closed under complementation.
  Example: $L=\{a^nb^nc^n\}$ not a CFL(a CSL) but, $\overline{L}$ is and in-fact can be solved using a NPDA (construct a NPDA where it checks for either $\text{Number}_a \neq \text{Number}_b$ or $\text{Number}_b\neq \text{Number}_c$ or $\text{Number}_a \neq \text{Number}_c.$ But we can’t construct one which can check $\text{Number}_a = \text{Number}_b = \text{Number}_c)$
• Intersection or Union of a CFL and RL always gives a CFL. So it is closed under the same.

---

Now,

• A. $L_2$ is complemented so, needn’t be a CFL.
• B. $\overline{\overline{L_1}\cup\overline{L_2}}=L_1\cap L_2$ intersection of a CFL and RL is a CFL
• C. $L_1\cup(L_2\cup\overline{L_2})=L_1\cup(\Sigma^*)=\Sigma^*$  hence a CFL.
• D. $(L_1\cap L_2)\cup(\overline{L_1}\cap L_2)=L_2$  or it’s a union of two CFLs if you don’t bother to solve.

Comments

lol :’)

---

Kanwae Kan

Now perfect👍

---

NICE

Answer 2

The options should be $b,c,d$. 

Options –

(a) The Complement of CFL is Recursive. The intersection of Recursive and Regular is Recursive.

(b) It is $L_1 \cap L_2$ and intersection of CFL and regular is CFL.

(c) It is $\Sigma^*$ itself as $L_2  \cup \bar{L_2}$ is $\Sigma^*$ and union of $\Sigma^*$ and $L_1$ is $\Sigma^*$ which is regular and thus CFL.

 (d) Solving this you will get $L_2$ which is CFL. See the image below.

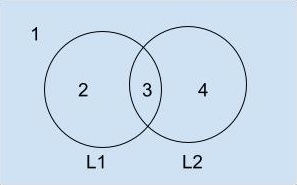
We can write the $(d)$ option as,

$= (23 \cap 34) \cup (14 \cap 34)$

$= (3) \cup (4)$

$= L_2$

Comments

in option D both are CFL ( regular intersection with CFL)   union of two CFL is CFL

---

The intersection of Recursive and Regular is Recursive.

How??

Is this because Regular language is a subset of Rec. language and therefore, regular language can be written as Recursive language, and hence we can say intersection of recursive language with recursive langauge is recursive(since, recursive languages are closed under intersection.)

---

@`JEET Sir,

Yes , that’s  the exact reason.