GATE CSE 2021 Set 2 | Question: 1

Question

Let $G$ be a connected undirected weighted graph. Consider the following two statements.

• $S_1$: There exists a minimum weight edge in $G$ which is present in every minimum spanning tree of $G$.
• $S_2$: If every edge in $G$ has distinct weight, then $G$ has a unique minimum spanning tree.

Which one of the following options is correct?

• A. Both $S_1$ and $S_2$ are true
• B. $S_1$ is true and $S_2$ is false
• C. $S_1$ is false and $S_2$ is true
• D. Both $S_1$ and $S_2$ are false

Comments

in this question s1 is false and s2 is true but in GO answer key it is showing s1 true s2 false

---

Counter-example for S1 → Consider a triangle, with each of the 3 edge-weights being equal – now 3 MSTs are possible here and in each of the 3 MSTs, 1 edge misses out, so no minimum weight edge is present in all the 3 MSTs.

---

$S1:$ is $true$ if edge weight are distinct  and $false$ if edge weight are same  

$S2:$ is $true$

Answer 1

We can think of running the Kruskals algorithm for finding the Minimum Spanning Tree on graph $G.$

While doing that, we sort the edges based on their weight and start selecting edges from the smallest weight $(w_{\text{small}}$ for example).

Problem with $S_1$:  If we have multiple copies of $w_{\text{small}}$, then a specific $w_{\text{small}}$ weighted edge is not guaranteed to be selected by Kruskals algorithm.

$S_2$ is Correct: If the sorted order of the edges contains only distinct values, Kruskals algorithm will always select a unique set of edges resulting in a unique minimum spanning tree.

Correct option: C.

Comments

going through a bunch of comments makes me feel that still, a min weight edge is definitely present as per your counterexample hence statement S1 is still holding as true...

---

I think the following.

“There exists a minimum weight edge” – about a specific edge

and ..

“There exists a minimum weight “ – about a specific weight value

---

Converse of S2 is NOT TRUE.

Answer 2

S1 is false -->If G has all edges with equal weight , then not possible,

S2 is true

Comments

I think it’s wrong to say ruins the question, it was already 1-marker, and any “serious” aspirant know about the concept where multiple MSTs are possible. May be it was expected to be straight forward and many ruined it by thinking more complicated cases.

---

Yes, it depends on the perspective.

---

Can you provide any example that given minimum edge is not selected. Kruskals will always pick the smallest edge weight. So that minimum edge will always be selected even though there exist multiple minimum spanning tree.

Answer 3

S1: “There exists a minimum weight edge in G”

There can be two interpretations of this statement-

1) There exists a specific minimum weight edge which must be present in all minimum spanning trees of the graph.

2) There exists atleast one minimum weight edge which is present in every minimum spanning trees of the graph.

In either case S1 will be false statement. Let me prove this using two examples.

For case 1

 

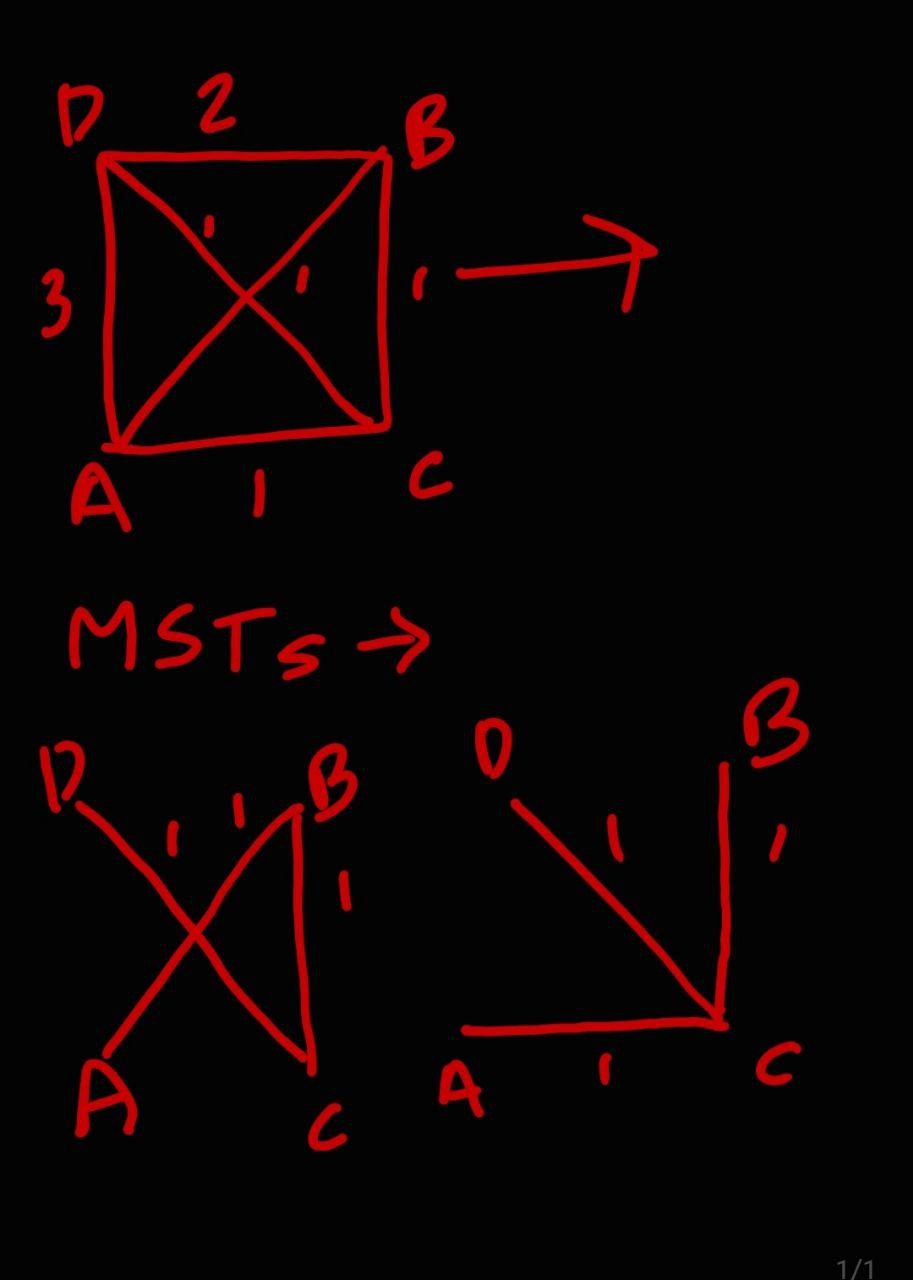
Here edge AB is not present in two of the possible minimum spanning trees.

For case 2

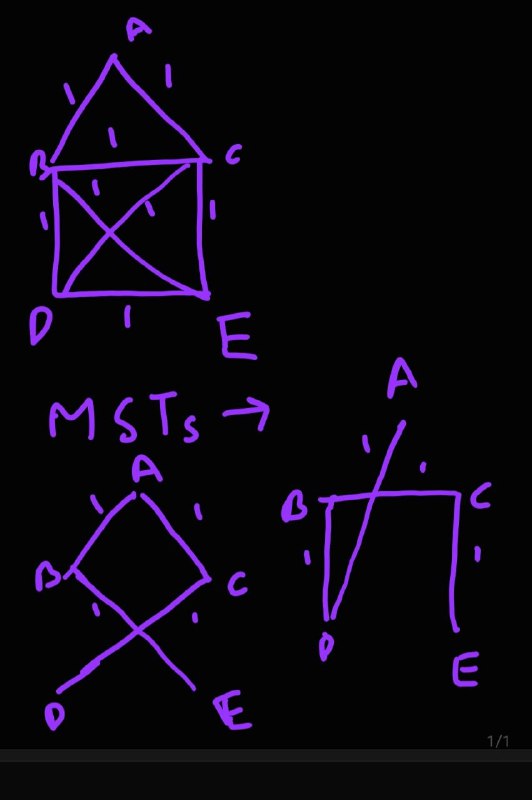
Here no edge is common between the two possible minimum spanning trees of the graph. That is there does not exist atleast 1 edge which is present in the two possible spanning trees.

So we can clearly state that Statement 1 is False.

S2: “If every edge in G has distinct weight, then G has a unique minimum spanning tree.”

This statement is obvious since if edge weights are distinct there will always be a distinct edge set and only 1 minimum spanning tree possible. Which is True

Correct Answer C

Answer 4

Since in S1 its not mentioned about the uniqueness of weights, assume in the graph where all edges have equal weights, then all the weights are minimum and not all minimum weights are included in spanning tree. Hence S1 is false.

 

In S2 all the edge weights are unique this means only 1 possible combination is there for making the spanning tree. Hence true.

So option C is correct

Comments

The answer should be, both S1 and S2 true. as per the language given in the question, you can’t make assumptions, i.e. there are multiple minimum weighted edges.