GATE IT 2005 | Question: 32

Question

An unbiased coin is tossed repeatedly until the outcome of two successive tosses is the same. Assuming that the trials are independent, the expected number of tosses is

• A. $3$
• B. $4$
• C. $5$
• D. $6$

Comments

3 ?? answer ?

---

Yes the given answer is 3.
Please explain the solution.

---

Is this https://gateoverflow.in/20011/tifr2011-a-6 (question) same as the above question? The method of solving is different but answer comes out same for first consecutive heads and comes out same for two consecutive tossess independent of heads or tails??

Please comment on this doubt.

---

@manoj

Yes you are correct we could solve like that

see my solution

---

For H and T simultaneously, we can refer to https://gateoverflow.in/69392/expectated-no-of-coin-toss .

---

Let $X$ be the random indicator variable indicating the No. of tosses required to get consecutive similar outcomes (HH/TT). We are asked to find $E[X]$.

Let $T1$, $T2$, ... denote the outcomes of tosses 1, 2, ... ($T1 = H$ if the first toss came out Heads, and so on).

 

Then, we need at least 1 toss for that. After $T1$, there can be two possibilities: either $T2 = T1$, or $T2 \neq T1$.

If Case I: $T2 = T1$,  then we are done; that is, we need only 1 more toss ($T2$).

So, Expected no. of tosses after $T1 = 1$.

 

If Case II: $T2 \neq T1$, then we are back at our original problem; that is, $T1$ was wasted and we need just as many more tosses (after $T1$), as were required before.

So, Expected no. of tosses after $T1$ = Expected no. of tosses before $T1 = E[X]$.

 

Note that Case I and Case II are both equally likely and have probabilities $1/2$ each.

So our equation becomes:

 

$E[X] = 1 + P($case $I)\cdot(1) + P($case $II) \cdot (E[X])$

$E[X] = 1 + (1/2) + (1/2)\cdot E[X]$

$E[X] = 3/2 + E[X]/2$

$E[X]/2 = 3/2$

$E[X] = 3$

 

If you're wondering how we can write such an equation, remember the concept of Linearity of Expectation.

---

https://math.stackexchange.com/questions/364038/expected-number-of-coin-tosses-to-get-five-consecutive-heads

A good read, specially the comments

---

$Ans: A$

---

K: Number of tosses till two successive tosses are same

$K=\dfrac{1}{4}\times 2+\dfrac{1}{4}\times 2+\dfrac{1}{4}\times (K+1)+\dfrac{1}{4}\times (K+1)$

$K=\dfrac{2+2+2K+2}{4}$

$2K=6$

$K=3$

---

@Kushagra गुप्ता

Your approach is correct. 👍

---

I am applying your approach for first HT.

When I am doing with your approach I am getting ans : 6, but original ans is 4.

K=(1/4)(K+2)+(1/4)(K+1)+(1/4)(K+1)+(1/4)(2)

4K=K+2+K+1+K+1+2

4K-3K=6

K=6.

Can I know where am going wrong ?

---

How it is k+1?

---

@Saikumar_Baalu

Where answer given as 4 ?

---

@Kushagra गुप्ता Please let me understand how its (K+1) Shouldnt it be K+2. We are doing two coin flips for Ht and TH right. 

---

https://www.youtube.com/watch?v=--mxW3jDlGk
 

@KUSHAGRA गुप्ता, see this video, here we are getting 4, for HT case.

---

When a toss begins with HT, the wasted flip is H. Whether T is a wasted flip or not, depends on the next flip. (Same explanation for TH) 

Like in HTT, the first T is not a wasted flip, but in HTH, the first T gets wasted. 

Hence, while writing the recurrence, (K+1) is written.

reference on wasted flips → https://www.codechef.com/wiki/tutorial-expectation

---

@KUSHAGRA गुप्ता @Pranavpurkar @ankitgupta.1729 While using the above method to solve An unbiased coin is tossed repeatedly and outcomes are recorded. What is the expected no of toss to get HT ( one head and one tail consecutively), I am  getting 6 as the answer, although the answer should be 4 as shown in the best answer. 

I found this method everywhere. Links : Monday Puzzle: Two Heads In A Row – Mind Your Decisions

probability - Expected Number of Coin Tosses to Get Five Consecutive Heads - Mathematics Stack Exchange

My process is:- 

Let $K$: Number of tosses till two successive tosses are same

Sample cases = HT, HH, T

So k = $(1/4)$*$2$+$(1/4)$*$(k+2)$+$(1/2)$*$(k+1)$

$\implies$ $4k = 2+k+2+2k+2\implies k=6$

I think I am making mistake in writing the equation. How do we calculate the wasted cases properly? @ankitgupta.1729 Sir.

---

@Abhrajyoti00 You probably mean $k$ as Expected number of tosses to get $HT$ and here, you have written:

$k = \frac{1}{4}*2 + \frac{1}{4}*(\textbf{k}+2) + \frac{1}{2}*(k+1)$

You are doing mistake while writing “k” in (k+2) in right side (made it as bold)

You have written $(k+2)$ because you would mean that we have wasted 2 coins in $HH$ and then repeat it again to get $HT$ but you will not have to repeat to get $HT,$ you have to flip a fair coin until you get $T$ because you have already got “H” in $HH$, so your motive here only to get one tail. And so, you have to write equation as:

$k = \frac{1}{4}*2 + \frac{1}{4}*(k’+2) + \frac{1}{2}*(k+1)$                    $(1)$

where $k’$ is the expected number of tosses to get $T.$ So,

$k’ = \frac{1}{2}*1 + \frac{1}{2} (1 + k’) \Rightarrow k’ = 2$

Hence from equation $(1),$

$k = \frac{1}{4}*2 + \frac{1}{4}*(2+2) + \frac{1}{2}*(k+1)$

$k=4$

---

@ankitgupta.1729 Sir, THANK YOU SO MUCH. This answer has cleared my doubts. I think I have more clarity in wasted turns now. Just one thing : The $\frac{1}{2}*1$ signifies that we got T at first toss only and $\frac{1}{2}*(1+k’)$ signifies that one turn was wasted because again H appeared instead of T right?  

Therefore we require two variables.

---

Yes. $(1+k’)$ shows we got head in 1^st turn (1 coin flip is wasted) and so we have to repeat again to get 1^st tail.

---

Ok! Last thing: We write $\frac{1}{4}*(k’+2)$ in equation $(1)$ so that:  “to get one T, expected no. of tosses is $k’$ else $2$ turns are wasted”. Is my reasoning correct @ankitgupta.1729 Sir?

---

yes. You have divided the cases like $HT,HH,T$. Now for $HH$, your motive is to get $HT$ but you got H at the end in HH already, so you only have to get “first” tail. So, you have to introduce one new variable, say, $k’$  in your equation and $+2$ shows you have wasted $2$ coin flips in $HH$. 

I have missed the word “first” while describing $k’.$ So,

$k’$ is expected number of tosses to get “first” tail.

All these things come from the Law of Total Expectation.

---

Thanks :)

---

self note – 

2 toss – HH , TT out of 4 ways

3 toss – THH , HTT out of 8 ways

4 toss – HTHH , THTT out of 16 ways

.

.

.

expected # of tosses

= 2*(2/4) + 3*(2/8) + 4*(2/16) ….….. ∞          is an agp

= 3

Answer 1

Probability on each branch  $= x = \frac{1}{2}$

2nd toss onwards, each toss layer gives us two success. (i.e. HH event or TT event ) 

$$\begin{align} E &= \sum k.p(k) \\ &= 2.(2x^2) + 3.(2x^3) + 4.(2x^4) + 5.(2x^5) + ... \\ &= 2.\left [ 2x^{2} + 3x^{3} + 4x^{4} + 5x^{5} + .... \right ] \\ &= 2.\left [ \frac{x}{(1-x)^2 } - x \right ] \\ \\ &\text{ putting x = } \frac{1}{2} \ \ \text{ ;}\\ \\ &= 2.\left [ \frac{\frac{1}{2}}{\left(\frac{1}{2}\right )^2} - \frac{1}{2} \right ] \\ &=3 \end{align}$$

---

A very similar QS :

An unbiased coin is tossed repeatedly and outcomes are recorded. What is the expected no of toss to get HT ( one head and one tail consecutively) ?

 

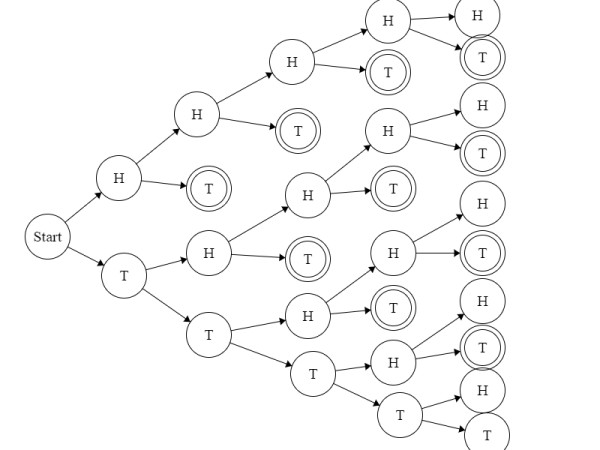
Probability in each branch $=0.5$. I double circled the satisfying toss events.
While observing the diagram I noticed that, from 2nd toss onward our required event starts showing up. Additionally,

 1. in the $\text{2nd}$ toss (or the 3rd level) we have one satisfying case.
 2. in the $\text{3rd}$ toss (or the 4th level) we have two satisfying case.
 3. in the $\text{4th}$ toss (or the 5th level) we have three satisfying case.
 4. in the $\text{5th}$ toss (or the 6th level) we have four satisfying case.
 5. etc.

i.e. in the $\text{kth}$ toss we would have $(k-1)$ satisfying case.
So,

$$\begin{align} E(x) &= \sum_{k=2}^{\infty } k.P(k)\\\ &= \sum_{k=2}^{\infty } k.\left \{ (k-1)*(0.5)^k \right \}\\ &= \sum_{k=2}^{\infty } \left \{ (k^2-k)*(0.5)^k \right \}\\ \end{align}$$

Using geometric series identity : https://en.wikipedia.org/wiki/Geometric_series#Geometric_power_series

$$\begin{align} \sum_{k=2}^{\infty}k(k-1)x^{k-2} = \frac{2}{(1-x)^3}\ \ \text{for } |x| < 1 \\ \end{align}$$

In our case : $x = 0.5$ So,

$$\begin{align} E &= \sum_{k=2}^{\infty}k(k-1)x^{k} = x^2\sum_{k=2}^{\infty}k(k-1)x^{k-2} = x^2.\frac{2}{(1-x)^3} \\ \end{align}$$

putting $x = \frac{1}{2}$   ; we get $E = 4$

---

More example:

For consecutive two heads ; HH

By drawing the tree diagram we can find the following series :

 

$$\begin{align*} E &= \sum{k.P(k) } \\ &=2.(1.x^2) + 3.(1.x^3) + 4.(2.x^4) + 5.(3.x^5)+6.(5.x^6)+7.(8.x^7)+.....\infty\\ \end{align*}$$

Above series is a nice combination of AP , generating function and Fibonacci numbers !!!!

• AP terms can be handled by integration or differentiation
• Fibanacci Generating function is = $\begin{align*} \frac{1}{1-x-x^2} \end{align*}$

 $$\begin{align} &\Rightarrow \frac{E}{x} =2.(1.x^1) + 3.(1.x^2) + 4.(2.x^3) + 5.(3.x^4)+6.(5.x^5)+7.(8.x^6)+.....\infty\\ &\Rightarrow \int \frac{E}{x} .dx = 1.x^2+1.x^3+2.x^4+3.x^5+5.x^6+.....\infty \\ &\Rightarrow \int \frac{E}{x} .dx = x^2.\left ( 1.x^0+1.x^1+2.x^2+3.x^3+5.x^4+.....\infty \right ) \\ &\Rightarrow \int \frac{E}{x} .dx = \frac{x^2}{1-x-x^2} \\ &\Rightarrow \frac{E}{x} = \frac{\mathrm{d}}{\mathrm{d} x}\left [ \frac{x^2}{1-x-x^2} \right ] \\ &\Rightarrow \frac{E}{x} = \frac{2x(1-x-x^2)+(1+2x)x^2}{(1-x-x^2)^2} \\ &\Rightarrow E = x.\left \{ \frac{2x(1-x-x^2)+(1+2x)x^2}{(1-x-x^2)^2} \right \} \\ &\Rightarrow E = \frac{1}{2}.\left \{ \frac{2.\frac{1}{2}(1-\frac{1}{2}-\frac{1}{4})+(1+2.\frac{1}{2}).\frac{1}{4}}{(1-\frac{1}{2}-\frac{1}{4})^2} \right \} \\ &\Rightarrow E = 6 \\ \end{align}$$

Infact 2nd QS on HT can also be done in the above way using integration.

Correct Answer: $A$

Comments

@Shreshta mam please explain how to solve second series?

---

Whoa...that HH variation came in GATE DA 2024

---

@strangelet_ So did you solve it ?

Answer 2

Answer is (A)

$E(X)= \sum X_{i} \times P_{i}$

Where X=no of tosses when you get successive HEAD/TAIL(only one is possible at a time though).

$P_{i}$=Probability that you get in $X_{i}$ tosses.

Now see solution:  

You need atleast 2 tosses to get 2 heads/tails. Now see if you throw twice probability to get 2 heads/tails is $\dfrac{1}{2}$ out of $4$ outcomes $[HT,HH,TH,TT].$

Similarly if you get result in $3rd$ toss that means you did not get in $2nd$ toss so favourable cases for this can be $THH$ and $HTT$ only out of total $8$ outcomes. So probability is $\dfrac{2}{8}=\dfrac{1}{2^{2}}.$

To generalize ,you can see that in every case you will have only two favourable cases and $2^{n}$ sample space. So for n th throw probability is $\dfrac{1}{(2^{n-1})}.$

Now coming to $E(X)= 2\times \dfrac{1}{2} + 3\times \dfrac{1}{4} + 4\times \dfrac{1}{8}+\ldots \text{till infinity}.$

See this is combined AP-GP, So multiplying E(X) by $\dfrac{1}{2}$ and subtracting from E(X).

$E(X)=2\times \dfrac{1}{2}+ 3\times {1}{4} +4 \times \dfrac{1}{8}+\ldots$

${0.5}\times E(X)=2\times \dfrac{1}{4} +3\times \dfrac{1}{8}+\ldots$

subtracting, we get $\frac{1}{2} \times E(X)= 1+\frac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\ldots$

${0.5} \times E(X)= 1+ \left(\dfrac{1}{4}\right)\div {\left(1-{0.5}\right)}= 1+\dfrac{1}{2} =\dfrac{3}{2}$             $\left(\frac{a}{1-r}\right)$

     $ E(x)= 3.$  

Comments

For subtraction part start subtraction from second term of E(X). You will get it right.

---

 doubt :

When I toss 3^rd time, that  means I definitely didn’t get HH or TT last time..so I think the sample space for third time should not include HHH ,HHT ,TTH ,TTT that means 

for 3^rd time favourable outcomes are HTT, THH only out of 2^3 – 4(removing not favourable) = 4 

so 3^rd time probability of getting two successive outcomes should be 2 / 4….but you are taking 2 /8 ?

 @Sandeep_Uniyal  can you please explain?

---

Explained very well. Thankyou.

Answer 3

Number of expected toss to get a head (or tail), E(H) = E(T) = 2

let the expected number of tosses to get two successive same outcome is e.

e = 1/2*(1+E(H)) + 1/2*(1+E(T))

e = 1/2*(1+2) + 1/2 *(1+2)

e = 3

 

Therefore correct answer would be (A).

 

Answer is right, but procedure is wrong.

Comments

Could you explain it a bit please !! I can't get your approach !!!

Thank You

---

Let the expected number of coin flips be x.

1. If first flip gives head and second gives tail then we have wasted 1 flip so need to do one more flip 

1/2 * 1/2 * (x+1)

2. If first flip gives head and second gives tail then we are done. (required 2 flips) So.

2(1/2 * 1/2)

3. If first flip gives tail and second head then wastage = 1 flip. (Same as 1st case)

1/2 * 1/2 * (x+1)

4. If both gives tail (same as 2)

2 (1/2*1/2)

so 

x = 2(1/2*1/2) + 1/2 *1/2 * (x+1) + 1/2 *1/2 *(x+1) + 2 * (1/2) * (1/2) 

x= 1 + (x +1 )/ 2

x= 3

---

why are we considering (pair of 2 tosses) flips here and not tosses seperately?

Answer 4

Let the expected number of coin flips be X.

The case analysis goes as follows:

a. If the first and second flips are HH or TT then we are done. The probability of this event is 2*(1/4) = 1/2

and the total number of flips required is 2.

b.if the first and second flips are TH or HT then we wasted 2 flips. The probability of this event is 2*(1/4) = 1/2

and the total number of flips required is X+2.

Adding, the equation  we get -
X=1/2(2)+1/2(X+2)

solving equation we get X = 3

answer : 3

Comments

@puja

HT or TH is a fail

case HT = prob of H =1/2 and prob of T=1..therefore 1/2...here 2 flips wasted (X+2)

case TH = prob of t =1/2 and prob of H=1..therefore 1/2...here also 2 flips wasted(X+2)

so X = (X+2)*1/2* (X+2) *1/2...but here shouldnt it be (X+2)*1/2  +   (X+2)*1/2 ??

am not sure if my understanding is correct

---

@MIRIYALA JEEVAN KUMA 

 I think that in case of HT or TH , it has wasted 1 flip.  So it should be x+1 but not X+2.

---

How are you getting x=3???? Im getting 4 , where im wrong😣