GATE CSE 2000 | Question: 7

Question

• A. Construct as minimal finite state machine that accepts the language, over $\{0,1\}$, of all strings that contain neither the substring $00$ nor the substring $11$.
• B. Consider the grammar
  • $S \to aSAb $
  • $S \to \epsilon $
  • $A \to bA $
  • $ A \to \epsilon $

  where $S$, $A$ are non-terminal symbols with $S$ being the start symbol; $a, b$ are terminal symbols and $\epsilon$ is the empty string. This grammar generates strings of the form $a^ib^j$ for some $i, j \geq 0$, where $i$ and $j$ satisfy some condition. What is the condition on the values of $i$ and $j$?

Answer 1

1. Language $L = (0+1)^*- (0+1)^*(00+11) (0+1)^*$
   $\textsf{DFA}$ contains $4$ states of which $3$ are final and $1$ is dead state.
   
2. $i \leq j$
   as $S \rightarrow aSAb$ 
   There will be always one $a$ in left and minimum one $b$ in right and $A  \rightarrow bA \mid \epsilon$ can generate any number of $b\text{’}$s including null string. If $A$ is $\epsilon$ then $i=j$ and if $A$ is generating any $b,$ then $j>i$ so  condition is $i\leq j.$

Comments

No. It's not related to this question. Actually, I came across somewhere and thought of writing that. 😁

---

Can anyone give the solution using the intersection of 2 DFA method? I am not getting a minimal solution.

---

First Negate The Given Statement : 

~(Strings that contain neither the substring $00$ nor the substring $11$) 

$\implies $ Strings that contain the substring $00$ or the substring $11$

So the regular expression is : $L’ = (0+1)^*(00+11) (0+1)^*$

Then drawing it’s DFA is very easy :-

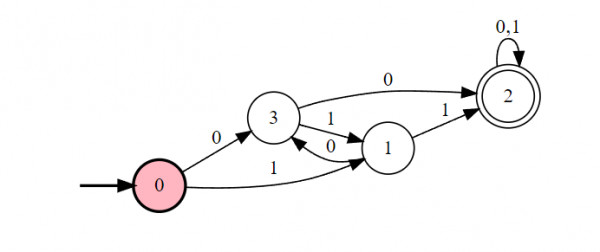
After this if you complement the machine (change all the final and non final states without touching the arrows), you will get the required min-DFA.

DFA made from : FSM Simulator (ivanzuzak.info)

Answer 2

j>=i is the condition.solve using some examples there will never be a condition when # of a's would be greater than # of b's