TIFR CSE 2019 | Part B | Question: 2

Question

How many distinct minimum weight spanning trees does the following undirected, weighted graph have ?

• A. $8$
• B. $16$
• C. $32$
• D. $64$
• E. None of the above

Comments

@air1ankit

Yes. The program will print any 1 of all possible spanning trees. 

I ran the algorithm to determine how many possible min spanning trees it can produce. What's wrong in that?

---

@gauravkc as per my knowledge if the edge weight is repeating or distinct edge have the same weight then there is possibilities to get 2 or more than two min spanning tree,

as you used kuruskal algorithms that is fine to get minimum spanning tree but you will get only one mst (if you run 1 time) but there are more possibilities right !  

and in question, they are asking #of mst not mst ... i don't knwo how you will determine all possibilities by kuruskal algo.

  

---

https://gateoverflow.in/276403/tifr-2019

Answer 1

There are $64$ minimum spanning trees possible.

Two choices for edge of weight $4$ for each of the outer triangle, i.e., $ \binom{2}{1}*\binom{2}{1}*\binom{2}{1}*\binom{2}{1}=2^4$ and two choices for edge of weight $2$ for each of the inner triangle i.e., $\binom{2}{1}*\binom{2}{1}=2^2$.

$2^4*2^2=64$

Comments

@Manoja Rajalakshmi A

Two choices for edge of weight 2 for each of the outer triangle, ie, (21)∗(21)∗(21)∗(21)=24(21)∗(21)∗(21)∗(21)=24 

It shouldn't be weight 4 instead of 2.?

Please explain your solution I'm not able to understand?

---

@Mayankprakash Two choices for edge weight $4$ (by mistake I wrote $2$)

Now consider one outer triangle which has two edges of weight $4$. Here we can take any one of the edge to form a minimum weight spanning tree, lly you can take the other edge also. So two choices for selecting an edge of weight $2$. There are $4$ such outer triangles, by fundamental theorem of counting we will get $2*2*2*2=16$  

---

@manoja
Thanks I got your approach.
1.I want to know whether it discards edges which can form cycle while considering and how do we neglect edges ?
2. Can we do this with Kirchoff law?

---

Yes you can but it will take so much time as we have to compute on 8 x 8 matrix

Answer 2

First we can write the edges in increasing order:

AD-1, AC-2, CD-2, AE-2, ED-2, AB-4, BC-4, CF-4, DF-4, DG-4, EG-4, HE-4, AH-4

 

 

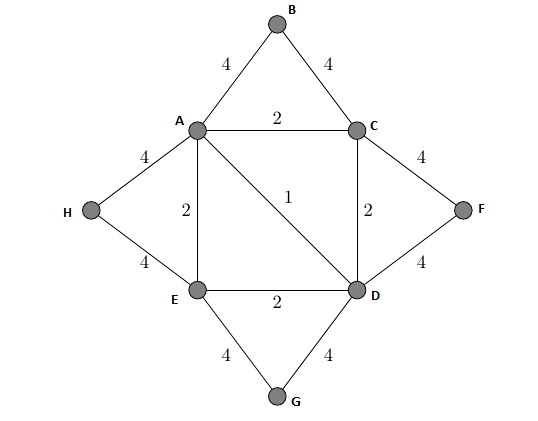
Now we have Vertices {A,B,C,D,E,F,G,H}

make sets by taking edges with min. weight:

 

1 weight- AD  Vertex cover: {A,D}

2 weight- Here we have 2 choice either AC or CD:   Vertex Cover {A,D,C} 

2 weight- Here we have 2 choice either AE or ED:   Vertex Cover {A,D,C,E} 

4 weight- Here we have 2 choice either AB or BC:   Vertex Cover {A,D,C,E,B} 

4 weight- Here we have 2 choice either CF or DF:   Vertex Cover {A,D,C,E,B,F}

4 weight- Here we have 2 choice either DG or EG:  Vertex Cover {A,D,C,E,B,F,G}

4 weight- Here we have 2 choice either HE or AH:   Vertex Cover {A,D,C,E,B,F,G,H}

 

Total distinct MST= $\binom{1}{1}*\binom{2}{1}*\binom{2}{1}*\binom{2}{1}*\binom{2}{1}*\binom{2}{1}*\binom{2}{1}$

Hence option (D).

 

 

Answer 3

 

 

any one please check whether it is a correct way or not?? 

i am also getting 64 

Comments

@srestha please check above explanation ..!

---

@Chaitrasj

https://gateoverflow.in/2019/gate2014-2-52

While answering this problem

These two are counted as distinct even though they are isomorphic.

Finding distinct spanning trees which are not isomorphic to each other is a very tough problem.

I don't think the question is to find that here. Even if it is non-isomorphic spanning trees the answer might not be 16

---

Yes, got it, thanks!

Answer 4

 

Total 64 MWSTs possible.

Answer : D