TIFR CSE 2019 | Part B | Question: 2

Question

How many distinct minimum weight spanning trees does the following undirected, weighted graph have ?

• A. $8$
• B. $16$
• C. $32$
• D. $64$
• E. None of the above

Comments

16?

---

I was getting 16 🤔

---

@Abbas2131 same!

---

oh yes ! thanks for correcting!!

---

first select the square to be dissolved :

 the edge of 1unit will always be there.

now from remaining 4edges of weight 2 you can select two edges such that it forms a tree in 4#ways...

also for each traingle at the edge of square you can only select one out of 2 edges of weight 4...  #ways = 2*2*2*2 = 16ways

therefore total number of spanning tres = 16*4 = 64

---

won't it be 64 as on either side of Edge with weight 1, there are 8 ways of choosing edges, so 8*8=64 ?

Out of triangle with weight 2- > select 1 edge (2 ways) , out of triangles with weight 4 -> select 1 edge (2 ways each)

there are 6 such triangles so 2*2*2*2*2*2 = 64

---

The graph is symmetric, so we can't take it as 64, all of them won't be distinct. Even I got 16 but was unsure

---

For the edge with weight 1 we have no choice it has to be included in the minimum spanning tree so for 2 vertices we have one edge.

Now for the remaining vertices , we have 4 vertices which are connected to someother vertices by an edge of minimum weight 2  out of which 2 vertices are already connected to each other by an egde of weight 1 so we have only 2 vertices left. So they have 2 options.So in all 2*2=4 for these vertices. But

4 vertices are connected to some other vertice of the graph by an edge of any weight 4 so they dont have anyother option but that of weight 4. For these edges there are 2 options . So 4*2 options for these edges are there . But as an edge impies 2 vertices no of distict ways this can be done is:4*2/2=4.

No of distinct spanning trees=4*4=16

---

which one not distinct @Chaitrasj

Can u check this https://gateoverflow.in/2019/gate2014-2-52

---

See with n=3 , there will be 3 spanning tree

Are they not symmetric?Yes

Still 3 spanning tree

with n=4

there will be 16 spanning tree

for more https://www.geeksforgeeks.org/g-fact-20-cayleys-formula-for-number-of-labelled-trees/

So, here ans will be 64

---

Ma'am check this image, I meant that if we draw it this way choosing different edges for making tree, still both the structures are isomorphic so they both are same and we are asked for distinct. (I have numbered the vertices here to show similarity, in q it's unlabbed vertices)

In the geeksforgeeks link, it is talking about labelled vertices, in this question input graph is having unlabelled vertices

In the previous gate question, the given graph is not symmetric, here the input graph is symmetric about the diagonal line with edge 1, hence I thought if we go by the method used in previous gate question to solve, it would lead to some duplicate trees.. thanks

---

I think answer must be 64

If you apply kruskal's algorithm.

edge with 1 with be selected. No choice.

For edges with weight 2, there are 4 choices. But adjacent edges won't be selected when the diagonal and 2 edges form a cycle(triangle).

We are left with 4 choices.

For the rest of 4 vertices, we have 2 choices for each. Hence $2^4$

$4*2^4=64$

---

@gauravkc but the choices made affect the other nodes too!

---

How?

Once any one out of 4 choices is made for inner square, we are sure the inner 4 vertices (that form the square are connected)

In the surrounding 4 triangles, none of them will form cycle since I'm selecting only 1 edge out of the 2 slanting edges.

---

@Arjun Sir please provide your inputs on this question.

---

@gauravkc why are you applying kuruskal algo here , -

Kruskal's algorithm uses the greedy approach for finding a minimum spanning tree.

not to find the number of distinct minimum spanning tree.

---

@air1ankit

Yes. The program will print any 1 of all possible spanning trees. 

I ran the algorithm to determine how many possible min spanning trees it can produce. What's wrong in that?

---

@gauravkc as per my knowledge if the edge weight is repeating or distinct edge have the same weight then there is possibilities to get 2 or more than two min spanning tree,

as you used kuruskal algorithms that is fine to get minimum spanning tree but you will get only one mst (if you run 1 time) but there are more possibilities right !  

and in question, they are asking #of mst not mst ... i don't knwo how you will determine all possibilities by kuruskal algo.

  

---

https://gateoverflow.in/276403/tifr-2019

Answer 1

There are $64$ minimum spanning trees possible.

Two choices for edge of weight $4$ for each of the outer triangle, i.e., $ \binom{2}{1}*\binom{2}{1}*\binom{2}{1}*\binom{2}{1}=2^4$ and two choices for edge of weight $2$ for each of the inner triangle i.e., $\binom{2}{1}*\binom{2}{1}=2^2$.

$2^4*2^2=64$

Comments

@Manoja Rajalakshmi A

Two choices for edge of weight 2 for each of the outer triangle, ie, (21)∗(21)∗(21)∗(21)=24(21)∗(21)∗(21)∗(21)=24 

It shouldn't be weight 4 instead of 2.?

Please explain your solution I'm not able to understand?

---

@Mayankprakash Two choices for edge weight $4$ (by mistake I wrote $2$)

Now consider one outer triangle which has two edges of weight $4$. Here we can take any one of the edge to form a minimum weight spanning tree, lly you can take the other edge also. So two choices for selecting an edge of weight $2$. There are $4$ such outer triangles, by fundamental theorem of counting we will get $2*2*2*2=16$  

---

@manoja
Thanks I got your approach.
1.I want to know whether it discards edges which can form cycle while considering and how do we neglect edges ?
2. Can we do this with Kirchoff law?

---

Yes you can but it will take so much time as we have to compute on 8 x 8 matrix

Answer 2

First we can write the edges in increasing order:

AD-1, AC-2, CD-2, AE-2, ED-2, AB-4, BC-4, CF-4, DF-4, DG-4, EG-4, HE-4, AH-4

 

 

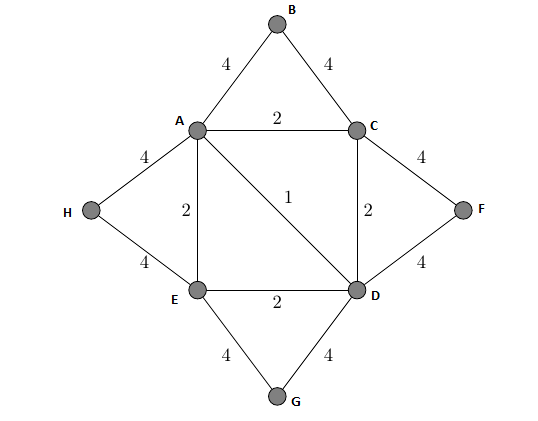
Now we have Vertices {A,B,C,D,E,F,G,H}

make sets by taking edges with min. weight:

 

1 weight- AD  Vertex cover: {A,D}

2 weight- Here we have 2 choice either AC or CD:   Vertex Cover {A,D,C} 

2 weight- Here we have 2 choice either AE or ED:   Vertex Cover {A,D,C,E} 

4 weight- Here we have 2 choice either AB or BC:   Vertex Cover {A,D,C,E,B} 

4 weight- Here we have 2 choice either CF or DF:   Vertex Cover {A,D,C,E,B,F}

4 weight- Here we have 2 choice either DG or EG:  Vertex Cover {A,D,C,E,B,F,G}

4 weight- Here we have 2 choice either HE or AH:   Vertex Cover {A,D,C,E,B,F,G,H}

 

Total distinct MST= $\binom{1}{1}*\binom{2}{1}*\binom{2}{1}*\binom{2}{1}*\binom{2}{1}*\binom{2}{1}*\binom{2}{1}$

Hence option (D).

 

 

Answer 3

 

 

any one please check whether it is a correct way or not?? 

i am also getting 64 

Comments

@srestha please check above explanation ..!

---

@Chaitrasj

https://gateoverflow.in/2019/gate2014-2-52

While answering this problem

These two are counted as distinct even though they are isomorphic.

Finding distinct spanning trees which are not isomorphic to each other is a very tough problem.

I don't think the question is to find that here. Even if it is non-isomorphic spanning trees the answer might not be 16

---

Yes, got it, thanks!

Answer 4

 

Total 64 MWSTs possible.

Answer : D