$\dfrac{2y+1}{y+2}<1$
$\implies \dfrac{2y+1}{y+2} - 1<0$
$\implies \dfrac{2y+1-y-2}{y+2}<0$
$\implies \dfrac{y-1}{y+2}<0\:; y + 2 \neq 0$
$\implies \dfrac{y-1}{y+2}<0\:; y \neq -2$
Here, $\dfrac{\text{Numerator}}{\text{Denominator}}<0 \implies \left\{\begin{matrix} \text{Numerator}> 0\:\: \textbf{and}\:\: \text{Denominator} < 0 \\ \text{Numerator}< 0\:\: \textbf{and}\:\: \text{Denominator} >0 \end{matrix}\right.$
$\textbf{Case(i):}\:\text{Numerator}> 0\:\: \textbf{and}\:\: \text{Denominator} < 0 $
$\implies y-1>0$ and $y+2<0$
$\implies y>1$ and $y<-2$
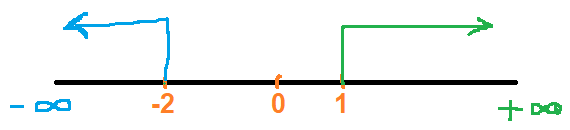
Here, nothing is common.
So, we can't express in the inequality form.
$\textbf{Case(ii):}\:\text{Numerator}< 0\:\: \textbf{and}\:\: \text{Denominator} > 0 $
$\implies y-1<0$ and $y+2>0$
$\implies y<1$ and $y>-2$
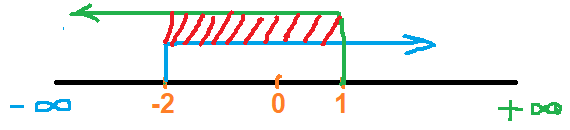
Here, ${\color{Red}{\text{Red}}}$ color shaded area is common.
$\therefore -2<y<1$
So, the correct answer is $(B).$