GATE CSE 2017 Set 1 | Question: 21

Question

Consider the Karnaugh map given below, where $X$ represents "don't care" and blank represents $0$.

 

Assume for all inputs $\left ( a,b,c,d \right )$, the respective complements $\left ( \bar{a}, \bar{b}, \bar{c}, \bar{d} \right )$ are also available. The above logic is implemented using $2$-input $\text{NOR}$ gates only. The minimum number of gates required is ____________ .

Answer 1

From K-map simplification we get the min-term as $CA'$. So We can simplyfy it for NOR gate expression

I.e. C' NOR $A = (C'+A)' = CA'$
Now complemented inputs are also given to us so, for $2$ input NOR gate we need only 1 NOR gate.

1 is correct answer .

Comments

can someone explain me with diagram how is the k-map reduced ? My answer is coming like : ca' + ac' which is by considering the two quad squares. Where am I wrong ? Why aren't we using the dont cares in first and fourth row ?

---

There isn't any requirement that don't cares MUST be used. If with the use of don't cares we can reduce the term size, only then a don't care need be used. 

---

@pranavg189

a group cant consist of all dont cares

---

This function has same $SOP$ and $POS$ form - $c.a$'
For $SOP$ - $c.a'$ is treated as single term.
For $POS$ - $c.a'$ is treated as 2 terms each of which is composed of a single variable.

---

Don't we need one nor gate for inverting the input "C" as well? So 2 NOR gates should be required in my opinion.

---

@Anshuman935

No need NOR gate for inverting the input because  it's available in the question.

And one more thing, OR-AND realization is equal to NOR-NOR realization, so it's better we write Product of sum (POS) form.

---

My POS form is (a + c).(a' + c') and I'm not getting a'.c Can someone write its POS form?

---

@habedo007

can you show your solution?

---

habedo007

I've done same mistake.

while computing POS, take don't care also to get the minimize POS form.

POS is A'C

---

if complemented inputs are not available then 2 NOR gates are required for $CA’$?? please verify.

$\overline{\overline {C\bar A}}\implies\overline{\bar C+A}$

---

@Hira Thakur yes, you’re correct.

Answer 2

Answer : 1 Only

Here we should take note that all inputs (a,b,c,d) and their respective complements are available.

And now when we solve the K-map the we get minterms like :

- >    cb'a'+ cba' 

- >    ca'(b+b')

- >    ca' 

If we give input to a NOR gate as c' and a the output will be (c' + a )' =  ca'.

So, only 1 NOR gate is Required.

Comments

the expression which comes is only ca'  how did u get cb'a'+cba' ????

---

ca' is the minimized form .
Check my answer again.

---

@Bikram sir check pls

if  question is max number of nor gate :

 (c' + a )'

term with a single literal  (c' ) requires an inverter 

(instead using inverter we can also  use nor gate to get this ) in this case max nor gate =2

---

See this  Shivam Chauhan

in this case max nor will be 2

Answer 3

Applying logic of k-map the simplified expression id ca'

now it is given that all inverted inputs are also available

so we can express ca' in terms of nor gate

(c'+a)'=ca'

so only 1 NOR gate required

1 is answer

ps: more editing will come

Answer 4

The expression of $K-map$ is $c.\bar a$

so the expression should be in $POS$ form for $NOR$ gate 

$\overline{\overline{c.\bar a}} = \overline{\bar c + a} $

Now the expression is in $POS$ form

NOTE : $\bar a , \bar a , \bar c \text { is given so no need to use NOT gate for that}$

 

 

So only 1 $NOR$ gate required

Comments

Actually the above method is more suitable when POS is given. But we got $a'+c$ which is sum term.

---

 $f(a,b,c,d) = \sum{(0,2,5,7,8,10,13,15)}$ Sum of Minterms(SOP)

$f(a,b,c,d) = \Pi{(0,2,5,7,8,10,13,15)}$ Product of Maxterms(POS)

Using $k-$map,we get

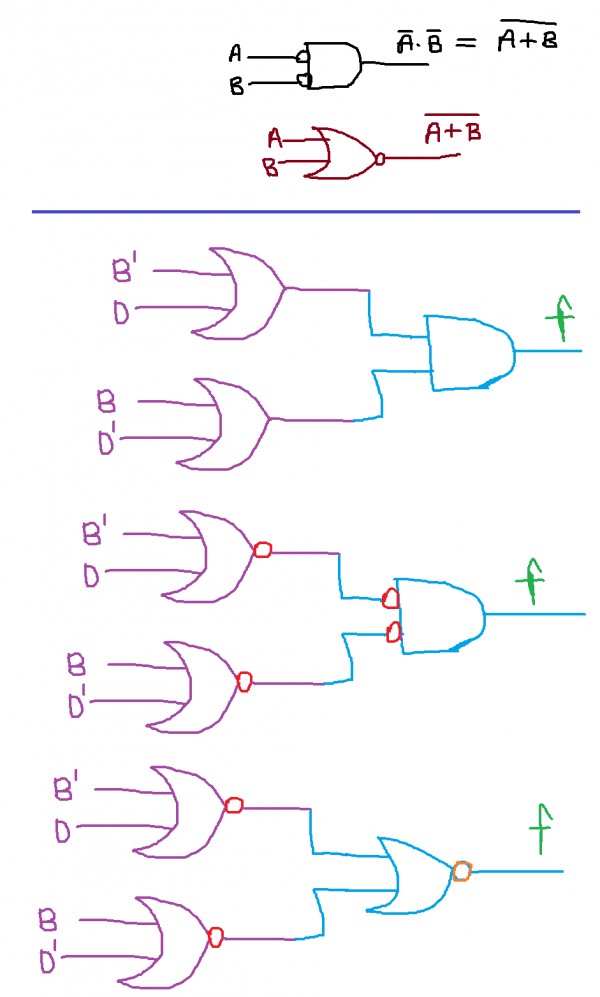
$f(a,b,c,d) = B'D'+BD$ (SOP)

$f(a,b,c,d) = (B'+D)\cdot(B+D')$ (POS)

Using the POS,we can easily make NOR gate.

---

We know,

Pos = (sop)'

Here sop expression is ca'

So converting to pos we get

(ca')' = (c'+a)

How you are applying double complement over the sop expression can u please explain?