[Self Doubt] Conversion of SR-flipflop to T-flipflop

Question

The standard approach for solving such problem is as follows:

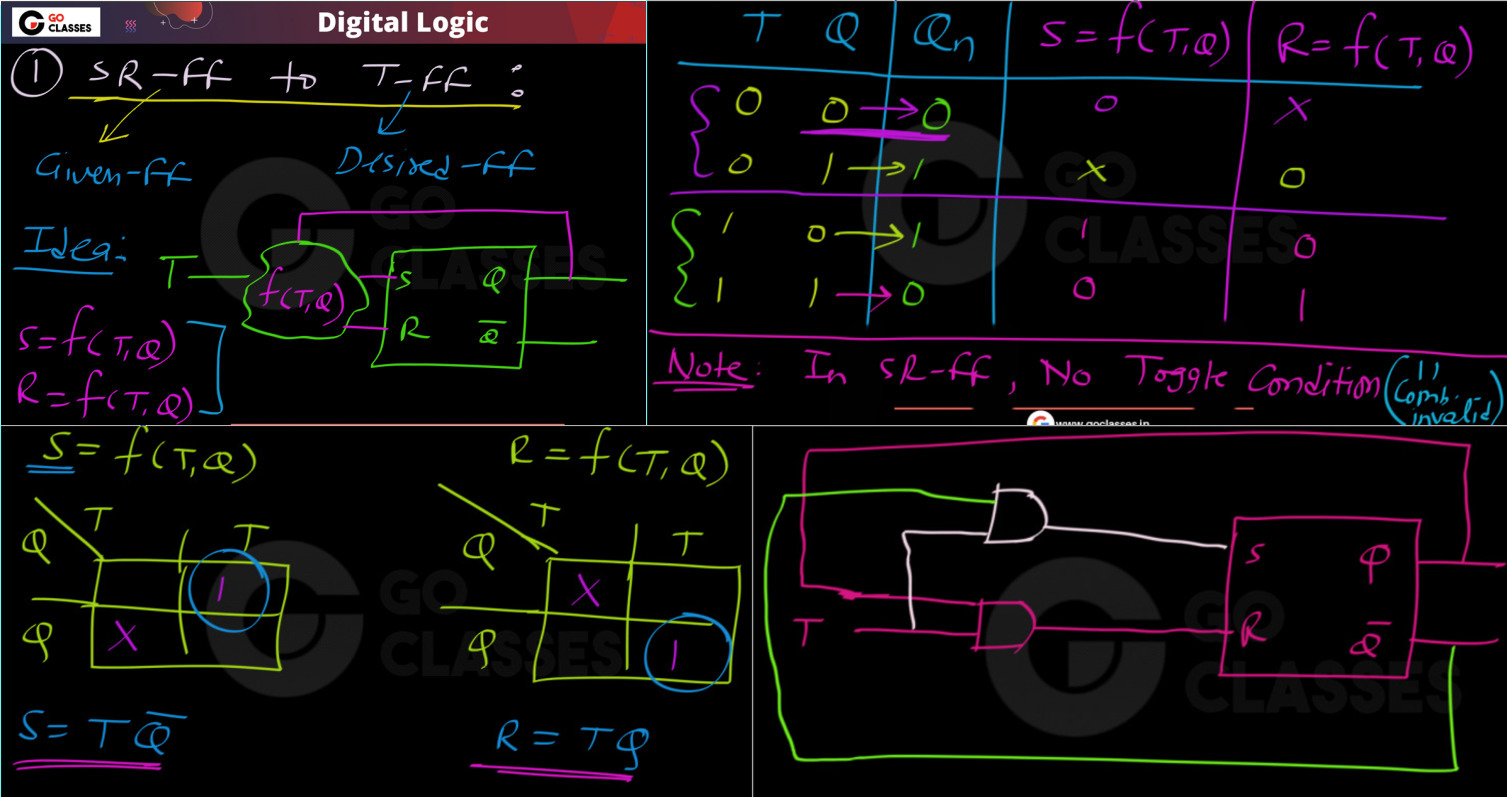
This approach gives us the equation for $S$ & $R$ in terms of $T, Q$ as
$S = T\overline Q \qquad \to (1)$

$R = TQ \qquad \to (2)$

---

I tried using a different approach for this conversion:

We know that the characteristic equation for SR-flipflop is,

$Q_n = S + \overline{R}Q \qquad \to (3)$ 

And the characteristic equation for T-flipflop is,

$Q_n = T\overline{Q} + \overline{T}Q \qquad \to (4)$

So, if in we put $S=T\overline{Q}$ and $R=T$ in $(3)$ then we would get the characteristic equation for a T-flipflop.

But in this approach, if we connect the inputs $S,R$ of an SR-flipflop to $T\overline{Q}$ and $T$ respectively then this allows for the $S=R=1$ input combination (when $Q = 0$) in the inner SR-flipflop, which is an undesirable state to be in.

However, with the standard approach, the $S=R=1$ input combination is never possible in the inner SR-flipflop.

Notice that with the standard approach if we substitute values of $S, R$ from $(1),\ (2)$ in $(3)$ then we get the characteristic equation of a T-flipflop ie., $(4)$.

So, what am I missing in my approach? Because at the end both approaches yield the same characteristic equation that is

$Q_n = T\overline{Q} + \overline{T}Q$ 

---

Adding a note here:

If we add the restriction $SR = 0$ to $Q_n = S + \overline{R}Q$ then that would give us

$Q_n = (S + \overline{R}Q)(\overline{S} + \overline{R}) = S\overline{R} + \overline{R}Q = \overline{R}(S + Q) \qquad \to (5)$

The characteristic eqn for T-ff: $Q_n = T\overline{Q} + \overline{T}Q = (\overline{T} + \overline{Q})(T+Q) \qquad \to (6)$

Now simply comparing the two eqn. $(5)$ &  $(6)$, we get $S = T$, $R = TQ$ but this arrangement allows the possibility for $S=R=1$ input combination in the inner SR-flipflop. So, we have to additionally keep in mind the $SR=0$ restriction while comparing the two equations.

eqn $(6)$ can also be written as $Q_n= (\overline{T} + \overline{Q})(T\overline{Q}+Q) \qquad \to (7)$

And now if we compare eqn. $(5)$ & $(7)$, we get $S=T\overline{Q}$ and $R=TQ$ which is consistent with the standard approach and maintains $SR=0$

Comments

@Deepak Poonia sir, please check this.

---

hey.

as per my understanding of digital logic i am trying to  give answer for this question.

as we know that  in SR flipflop

• we cannot give input as 11  now, the question is why we cannot give input as 11,
• so the simple is if we will give input as 11 then next output will be unpredicatable.
• it is not mean that we cannot give input as 11. but if we will give input as 11 then after that whatever output we will get for that vendor are not responsible means you can get unpredictalbe output.
• now so when we are desining SR flipflop then we should explictly mention that  11 input are not allow.
• -------------------------------------------------------------------------------------

 so if we are writing Q+=s+RbarQ then (we should also put disclamer that SR==11) not allow.
I hope this make sense to you
--------------------------------------------------------------------------------------------------
now lets come to this question if the Approch which you are using this will be correct if. there are no restriction on input

eg that

• JK to D conversion or vica versa (your approch and standard will give correct answer)
• NOW D to t  also gives correct answer.

now if you will make simple truth table for your approch then some how you will not be able to avoid SR==1.
 

here i wanted to attach an image .
but some how i can’t atatch becuase i donot know.

if you want we can discuess on telegram.

---

@thehitchh1ker, according to eq.2 , $R = TQ$. Then how can you substitute $R$ with $T$ in eq.3? are you assuming $R = T$?

---

@parth023
Above the first dotted line is the standard approach which gives us the equations $(1)$ & $(2)$.

Below it I have explained my approach which gives us $S=T\overline{Q}$ and $R=T$ by comparing eqn. $(3)$ & $(4)$